[BOJ-2579] Treppensteigen Problem und Dynamische Programmierung (Golang)

26. Mai 2025

Einführung

Tatsächlich war es ein Problem, dass ich mich so lange nicht mit dynamischer Programmierung beschäftigt habe. Als ich es früher getan habe, habe ich es nur grob verstanden und bin schnell darüber hinweggegangen. Aus diesem Grund konnte ich das Problem nicht einmal in Angriff nehmen.

Deshalb habe ich mir vorgenommen, dieses Mal die dynamische Programmierung gründlich zu studieren und habe versucht, das Problem zu lösen.

Dynamische Programmierung (Dynamic Programming)?

Dynamische Programmierung (Dynamic Programming, DP) ist eine Algorithmendesigntechnik, die Probleme in kleinere Teilprobleme zerlegt. Diese Technik wird hauptsächlich für Optimierungsprobleme verwendet und funktioniert, indem sie Memoisierung oder Tabellen verwendet, um frühere Berechnungsergebnisse zu speichern und erneut zu verwenden, um sich wiederholende Teilprobleme effizient zu lösen.

Dynamische Programmierung hat zwei Hauptmerkmale:

Optimale Teilstruktur (Optimal Substructure): Die optimale Lösung des Problems kann aus den optimalen Lösungen seiner Teilprobleme zusammengesetzt werden.
Überlappende Teilprobleme (Overlapping Subproblems): Das gleiche Teilproblem kann mehrfach berechnet werden.

Ein typisches Beispiel für die Berechnung der Fibonacci-Folge. Die Fibonacci-Folge hat die folgende Rekursionsformel:

$f(n) = f(n - 1) + f(n - 2)$

Die Lösungsmethoden sind Top-Down und Bottom-Up. Der Unterschied besteht darin, dass die Top-Down-Methode Rekursion verwendet, um Teilprobleme zu lösen, während die Bottom-Up-Methode Schleifen verwendet.

Wenn wir die Berechnung der Fibonacci-Folge mittels dynamischer Programmierung in Code darstellen, sieht das wie folgt aus:

Top-Down Ansatz

package main


import "fmt"
var memo = make(map[int]int)

func fibonacci(n int,) int {
    if n <= 1 {
        return n
    }
    if val, exists := memo[n]; exists {
        return val
    }
    memo[n] = fibonacci(n-1) + fibonacci(n-2)
    return memo[n]
}

func main() {
    n := 10
    result := fibonacci(n)
    fmt.Println("Fibonacci(", n, ") =", result)
}

Bottom-Up Ansatz

package main

import "fmt"

func fibonacci(n int) int {
    if n <= 1 {
        return n
    }
    fib := make([]int, n+1)
    fib[0], fib[1] = 0, 1
    for i := 2; i <= n; i++ {
        fib[i] = fib[i-1] + fib[i-2]
    }
    return fib[n]
}

func main() {
    n := 10
    result := fibonacci(n)
    fmt.Println("Fibonacci(", n, ") =", result)
}

Wenn wir den Kern-Algorithmus betrachten, verwendet die Top-Down-Methode Rekursion und die Memoisierungstabelle memo, um sich wiederholende Teilprobleme zu lösen, während die Bottom-Up-Methode Schleifen verwendet, um die Teilprobleme zu lösen.

Was, wenn man keine Memoisierung verwendet?

Tatsächlich ist es kein Problem, die Probleme ohne Memoisierung zu lösen. Allerdings gibt es bei den Problemen, die sich für die dynamische Programmierung eignen, immer wieder sich wiederholende Teilprobleme, sodass sich die Zeitkomplexität exponentiell erhöht, wenn keine Memoisierung eingesetzt wird.

Lassen Sie uns ein Beispiel betrachten.

Wie könnte man den bestimmten Wert $f(5)$ der Fibonacci-Folge berechnen?

Das lässt sich wie folgt ausdrücken: $f(5) = f(4) + f(3)$

Um f(4) zu berechnen, könnte man es so formulieren: $f(4) = f(3) + f(2)$

Jetzt schauen wir uns die beiden Gleichungen an. Der auffällige Teil ist $f(3)$ . $f(3)$ wird zweimal aufgerufen, um die Werte von $f(4)$ und $f(5)$ zu berechnen.

Während bei der Fibonacci-Folge die maximale Anzahl an Wiederholungen auf 2 begrenzt ist, kann die Anzahl an Wiederholungen in anderen dynamischen Programmierungen bei Bedarf exponentiell ansteigen.

In Anbetracht dieser Anmerkungen wollen wir das folgende Problem lösen: Treppensteigen.

Problem

BOJ-2579

Das Treppensteignspiel ist ein Spiel, bei dem man vom Startpunkt am Fuße der Treppe bis zur Endstelle an der Spitze der Treppe gelangt. An jedem Sprossen steht eine bestimmte Punktzahl, die man erhält, wenn man die Sprosse betritt.

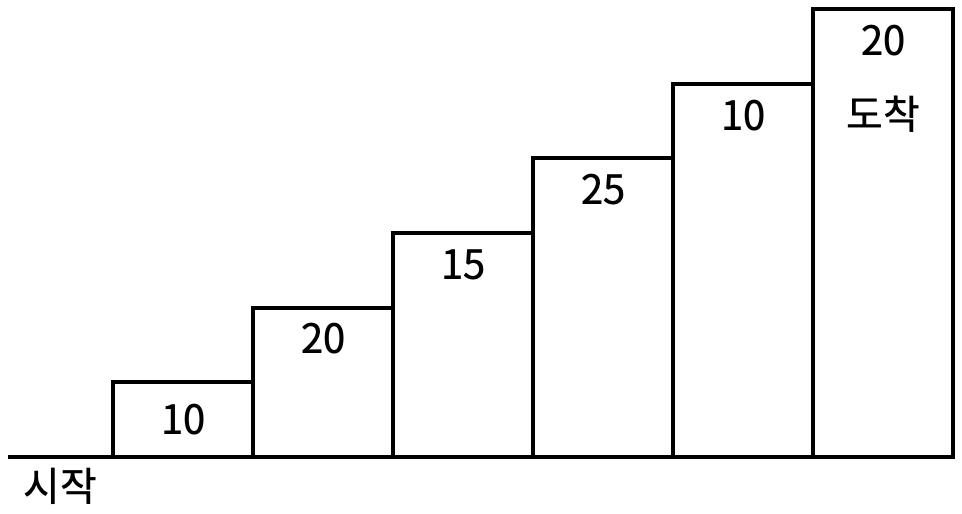
<Bild 1>

Wenn wir zum Beispiel von dem Startpunkt, indem wir die erste, zweite, vierte und sechste Sprosse besteigen, zu einem Endpunkt gelangen, beträgt die Gesamtpunktzahl 10 + 20 + 25 + 20 = 75 Punkte.

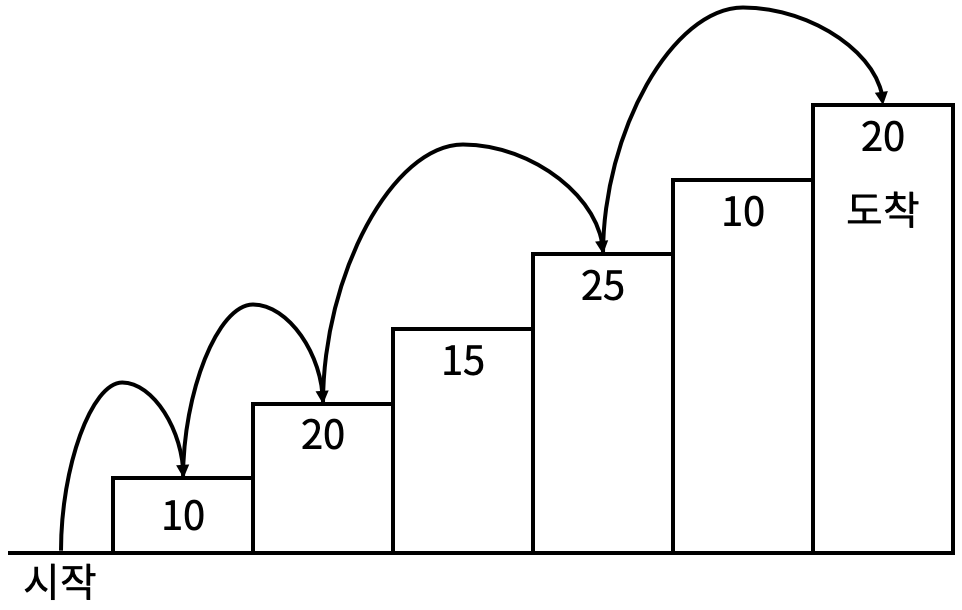
<Bild 2>

Es gibt folgende Regeln für das Treppensteigen:

Man kann eine Sprosse entweder einzeln oder im Sprung von zwei Sprossen überspringen. Das bedeutet, man kann eine Sprosse betreten und dann direkt zur nächsten Sprosse oder zur übernächsten Sprosse gehen.
Drei aufeinanderfolgende Sprossen dürfen jedoch nicht betreten werden. Punkten vom Startpunkt zählen nicht. Der letzte Schritt zur Abschluss-Sprosse muss auf jeden Fall angewendet werden. Deshalb kann man von der ersten Sprosse zur zweiten oder dritten Sprosse gehen, aber man kann nicht direkt von der ersten Sprosse zur vierten Sprosse springen oder alle drei Sprossen nacheinander betreten.

Wenn die Punktzahlen, die an jeder Sprosse angegeben sind, gegeben sind, schreiben Sie ein Programm, um die maximale Punktzahl zu finden, die in diesem Spiel erreicht werden kann.

Herangehensweise

Wenn ich das Problem grob lese, könnte ich denken, es sei einfach, alle Sprossen zu erklimmen, aber die Regeln des Treppensteigens, insbesondere das Verbot, drei aufeinanderfolgende Sprossen zu betreten, bilden den Kern des Problems.

Daher kann die Methode, Treppen zu steigen, grundsätzlich in zwei Fälle unterteilt werden:

Die aktuelle Sprosse wird betreten, ohne die vorherige Sprosse zu betreten, aber die vorvorherige Sprosse zu betreten.
Die aktuelle Sprosse wird betreten und die vorherige Sprosse wird betreten.

Um den Maximalwert zu ermitteln, müssen beide Fälle berücksichtigt werden.

Zunächst stellt sich die Frage, wie man den maximalen Punktwert auf der n-ten Sprosse ermitteln kann.

Wenn wir die oben genannten Fälle betrachten, können wir diese in zwei Fälle formulieren.

Fall 1: Wert der n-ten Sprosse + (Maximalwert bis zur (n-2)-ten Sprosse)

Fall 2: Wert der n-ten Sprosse + Wert der (n-1)-ten Sprosse + (Maximalwert bis zur (n-3)-ten Sprosse)

Der Grund, warum ich im zweiten Fall nicht einfach den Maximalwert bis zur (n-1)-ten Sprosse definiert habe, ist, um zu bestätigen, dass die (n-2)-te Sprosse nicht betreten wurde, als die (n-1)-te Sprosse betreten wurde.

Rekursionsformel

Diese können mithilfe der folgenden Rekursionsformel dargestellt werden:

$f(n) = ext{max}(f(n-2) + s(n), f(n-3) + s(n-1) + s(n))$

Hierbei ist $f(n)$ der Maximalwert auf der n-ten Sprosse und $s(n)$ der Punktwert der n-ten Sprosse.

Die Anfangswerte müssen den minimalen Werten zugewiesen werden, die die Zahlen in der Rekursionsformel erreichen können.

Das heißt, die Zahlen im Inneren der Funktion in der Rekursionsformel entsprechen den Indizes $n-1$ , $n-2$ , $n-3$ , daher müssen die Anfangswerte für die Indizes 0, 1, 2 wie folgt zugewiesen werden:

Daraus ergibt sich die gesamt Rekursionsformel:

$f(0) = s(0)$
$f(1) = s(0) + s(1)$
$f(2) = ext{max}(s(0) + s(2), s(1) + s(2))$
$f(n) = ext{max}(f(n-2) + s(n), f(n-3) + s(n-1) + s(n))$

Code

Der Code ist nicht sehr schwierig, nachdem die Rekursionsformel abgeleitet wurde.

In Übereinstimmung damit lautet der gesamte Code:

package main

import (
	"bufio"
	"fmt"
	"log"
	"os"
)

var memo = make(map[int]int)

func dp(stairs []int, n int) int {
	if value, ok := memo[n]; ok {
		return value
	}
	if n == 0 {
		return stairs[0]
	}
	if n == 1 {
		return stairs[0] + stairs[1]
	}
	if n == 2 {
		return max(stairs[0]+stairs[2], stairs[1]+stairs[2])
	}
	// zwei Treppen auf einmal
	case1 := dp(stairs, n-2) + stairs[n]
	// einmal einen Schritt nach oben
	case2 := dp(stairs, n-3) + stairs[n-1] + stairs[n]
	memo[n] = max(case1, case2)
	return memo[n]
}

func main() {
	writer := bufio.NewWriter(os.Stdout)
	reader := bufio.NewReader(os.Stdin)
	defer writer.Flush()

	var N int
	if _, err := fmt.Fscan(reader, &N); err != nil {
		log.Fatal(err)
	}

	stairs := make([]int, N)
	for i := 0; i < N; i++ {
		if _, err := fmt.Fscan(reader, &stairs[i]); err != nil {
			log.Fatal(err)
		}
	}

	fmt.Fprintln(writer, dp(stairs, N-1))
}

Github Quelle

https://github.com/YangTaeyoung/algorithm-go/blob/main/%EB%8B%A4%EC%9D%B4%EB%82%B4%EB%AF%B9%20%ED%94%84%EB%A1%9C%EA%B7%B8%EB%9E%98%EB%B0%8D/BOJ/2579/main.go

[Programmers] Joystick (Golang)