[プログラマーズ] ジョイスティック (Golang)

2025年5月26日

問題

ジョイスティックでアルファベットの名前を完成させてください。最初はAで構成されています。
ex) 完成させなければならない名前が三文字ならAAA、四文字ならAAAA

ジョイスティックを各方向に動かすと、以下のようになります。

▲ - 次のアルファベット
▼ - 前のアルファベット (Aから下に移動するとZに)
◀ - カーソルを左に移動 (最初の位置から左に移動すると最後の文字にカーソル)
▶ - カーソルを右に移動 (最後の位置から右に移動すると最初の文字にカーソル)
例えば以下の方法で"JAZ"を作成できます。

- 最初の位置でジョイスティックを上に9回操作してJを完成させます。
- ジョイスティックを左に1回操作してカーソルを最後の文字の位置に移動させます。
- 最後の位置でジョイスティックを下に1回操作してZを完成させます。
したがって11回移動させて"JAZ"を作成でき、これが最小移動です。
作りたい名前nameが引数として渡されたとき、名前に対するジョイスティック操作回数の最小値を返すようにsolution関数を作成してください。

この問題はコーディングテスト練習のパートでLEVEL2に分類されていますが、実際にはなぜLEVEL2なのか疑問に思うほど、思ったより私には難しい問題でした。

~~私にはLEVEL3程度でした。~~

アプローチ

この問題は大きく2つのパートに分けることができます。

ジョイスティックを上下に動かしてアルファベットを完成させる部分
ジョイスティックを左右に動かしてカーソルを移動する部分

思ったより1番は簡単ですが、2番は考えよりも難しいです。

1. ジョイスティックを上下に動かしてアルファベットを完成させる部分

ジョイスティックを上下に動かしてアルファベットを完成させる部分は思ったより簡単です。正順/逆順の2つを考慮しながら最小値を求める方法でアプローチすればいいです。

package main

func min(arr ...int) int {
	value := arr[0]
	for _, n := range arr {
		if n < value {
			value = n
		}
	}
	return value
}

func solution(name string) int {
	verticalMove := 0
	for _, alpha := range name {
		asc := int(alpha - 'A')
		desc := int('Z' - alpha + 1)
		verticalMove += min(asc, desc)
	}
	
	// ... 略
}

初期値は文字列の長さ分だけAで埋められているとのことです。したがって正順基準の場合、もしAなら0になり、Bなら1になります。 ASCII値を利用して簡単に計算することができ、alpha-'A'ならalphaがAなら0、Bなら1、Cなら2になるため、条件を満たすことができます。

逆順の場合はZ - alpha + 1で計算できます。例えばZの場合、もし'Z' - alphaだけだとZ-Zなので0になりますが、ジョイスティックなので1回の操作が必要なため+1します。

ここで私はmin関数を追加で定義しました。実際、min関数はGoの標準ビルトイン関数でもありますが、プログラマーズではGo 1.16.9という非常に古いバージョンを使用しているため、直接定義せざるを得ません。

参考までにmin関数はGo 1.21バージョンから標準ビルトイン関数として提供されます。

2. ジョイスティックを左右に動かしてカーソルを移動する部分

この部分で私は思ったよりも苦労しました。

~~そのためChatGPTから助けを受けたので、この反省の投稿を作成しています。~~

問題は連続したAの存在ですが、初期値としてAを自動的に埋めるという問題の条件があるため、ジョイスティックを動かす方向によってカーソルが移動すべき最小値が異なる可能性があるという点です。

例ケース: `AAAA`

AAAAという名前を書くとしましょう。

この場合、名前を書く必要がありません。すでにAで埋められているからです。

例ケース: `AABA`

それではAABAという名前を書いてみましょう。

この場合、左に動かす場合と右に動かす場合の2つの方法があります。

左に動かした場合、AAまではすでに完成されているため、▶カーソルを2回動かした後、アルファベットを変更する▲カーソルを1回でAABAを完成させることができます。合計3回の操作が必要です。

右に動かす場合、AABAを完成させるためには、カーソルを左に1回動かした後、▲カーソルを1回でAABAを完成させることができます。合計2回の操作が必要です。

それなりに単純な例ですが、より複雑な例も考えられます。

例ケース: `BBBAAAAAAAAAB`

例えば、BBBAAAAAAAAABという名前を書くとしましょう。前の例のように正順に行くと、▲カーソル2回、▶カーソル11回、▲カーソル1回で合計14回の操作が必要になります。

逆順に行くだけなら、▲カーソル2回、◀カーソル11回、▲カーソル1回で合計14回の操作が必要です。

ただし、BBBまで入力して戻るとどうなるでしょうか？この場合、Bを変更するためのカーソル▲3回、正順にカーソルを移動するための▶2回、再び戻って最後のBに移動するためのカーソル◀3回、最後のBを変更するための▲1回で合計9回の操作が必要になります。

では、逆順を最初に移動して再び戻るとどうなるでしょうか？

この場合、最後のBに移動するためのカーソル◀1回、Bを変更するための▲1回、正順にカーソルを移動するための▶1回、Bを変更するためのカーソル▲3回、右にカーソルを移動するための▶2回で合計8回の操作が必要になります。

このように、ジョイスティックに左右の移動は連続するAと位置によって最小値が異なる可能性があります。

そのため、この部分を解決するためには、毎回カーソルを移動する際に、次のAが出るまでカーソルを移動させる方法とその反対の方法をすべて考慮し、貪欲法的に最小値を求める必要があります。

コード

この部分はコードを先に見て、一つ一つ見ていきましょう。

package main

func solution(name string) int {
    // ... 略
	horizontalMove := len(name) - 1
	for i := 0; i < len(name)-1; i++ {
		next := i + 1
		for next < len(name) && name[next] == 'A' {
			next++
		}
		// 右に行った後左に戻って左に移動する場合
		moveRightLeft := (i * 2) + (len(name) - next)
		// 左に行った後右に戻って右に移動する場合
		moveLeftRight := (len(name)-next)*2 + i

		horizontalMove = min(horizontalMove, moveRightLeft, moveLeftRight)
	}
	// ... 略
}

まず、horizontalMoveの最大値はlen(name) - 1です。これは方向変更なしでカーソルを最初の位置から最後の位置に移動させる場合を意味します。

horizontalMove := len(name) - 1

その後nextを指定します。nextがAの場合、Aが終わるまでカーソルを移動し、nextとiの差を利用して最少カーソル移動回数を求めることになります。

next := i + 1
for next < len(name) && name[next] == 'A' {
	next++
}

その後moveRightLeftとmoveLeftRightを求めます。

// 右に行った後左に戻って左に移動する場合
moveRightLeft := (i * 2) + (len(name) - next)
// 左に行った後右に戻って右に移動する場合
moveLeftRight := (len(name)-next)*2 + i

名前にもわかるように、moveRightLeftは右からiだけ行った後、再びiだけ戻り、左にlen(name) - nextだけ移動する場合を意味します。

下の図で見れば、もっと簡単に理解できるでしょう。

図の1、2番はそれぞれiだけ移動し、3番はlen(name) - nextだけ移動する場合を意味します。

moveLeftRightは左にlen(name) - nextだけ行った後、またlen(name) - nextだけ戻り、右にiだけ移動する場合を意味します。

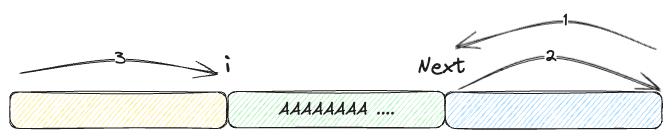
図の1、2番はそれぞれlen(name) - nextだけ移動し、3番はiだけ移動する場合を意味します。

したがって、最終的にhorizontalMoveを求める上記アルゴリズムは、次のような場合の中で最小値を探すアルゴリズムであると言えます。

一方向だけ移動する場合: len(name) - 1
各インデックスiで右に移動してから左に戻る場合: (i * 2) + (len(name) - next)
各インデックスiで左に移動してから右に戻る場合: (len(name)-next)*2 + i

こうすることで、最終的にはnameに対するすべてのインデックスでのジョイスティック操作に対する最小値を求めることができます。

最終コード

package main

import "fmt"

func min(arr ...int) int {
	value := arr[0]
	for _, n := range arr {
		if n < value {
			value = n
		}
	}
	return value
}

func solution(name string) int {
	verticalMove := 0
	for _, alpha := range name {
		asc := int(alpha - 'A')
		desc := int('Z' - alpha + 1)
		verticalMove += min(asc, desc)
	}

	horizontalMove := len(name) - 1
	for i := 0; i < len(name)-1; i++ {
		next := i + 1
		for next < len(name) && name[next] == 'A' {
			next++
		}
		// 右に行った後左に戻って左に移動する場合
		moveRightLeft := (i * 2) + (len(name) - next)
		// 左に行った後右に戻って右に移動する場合
		moveLeftRight := (len(name)-next)*2 + i

		horizontalMove = min(horizontalMove, moveRightLeft, moveLeftRight)
	}

	return verticalMove + horizontalMove
}

func main() {
	case1 := solution("JEROEN")
	fmt.Println(case1)
	case2 := solution("JAN")
	fmt.Println(case2)
}

[プログラミング] 入国審査 (Golang)[BOJ-2579] 階段登り問題と動的プログラミング (Golang)