[BOJ-9934] 完全二分木 (Golang)
概要
転職を準備しながら、久しぶりに木のアルゴリズムを勉強することになり、投稿することになった。
完全二分木の問題は、中間順序の配列を通じて完全二分木の形を知り、それを出力する問題で、まず中間順序という概念を理解しておく必要がある。
中間順序
前順/中順/後順の基準はノードの視点を見て判断する。
ノード -> 左の部分木 -> 右の部分木の順番で行うと、ノードが前にあるので前順であり、
左の部分木 -> ノード -> 右の部分木の順番で行うと、ノードが真ん中にあるので中間順である。
左の部分木 -> 右の部分木 -> ノードの順番で行うと、ノードが最後に来るので後順である。
この中で調べる方法は中間順であり、順番を巡る例は次の画像のようである。
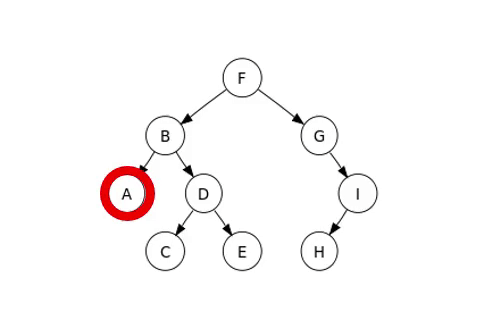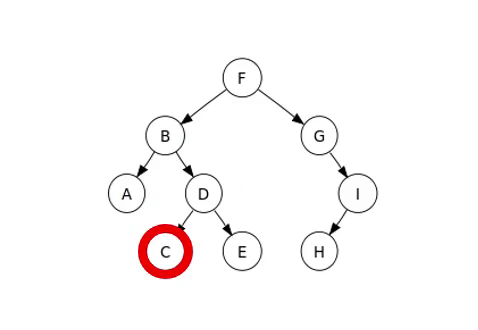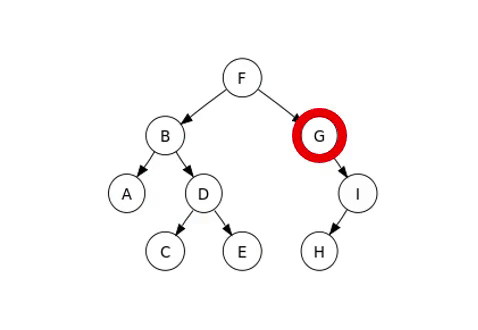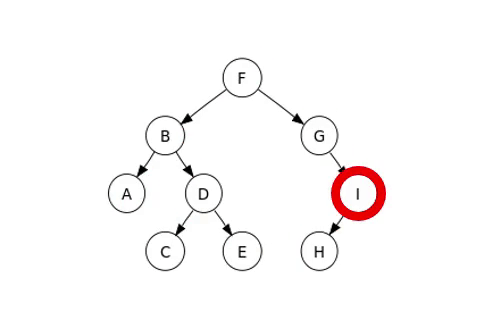
完全二分木
完全二分木は木のデータ構造があるとき、木の高さ hに対して全ノード数が 2^h-1を満たす二分木を言う。
二分木はすべてのノードの子の数が最大2つである木を意味する。
簡単に言えば、指定した高さに対してすべてのノードが満たされた状態の木を意味する。
例えば、高さが1の下記の木は単純に下のようにノードが一つだけある場合である。
ノードの個数 = 2^1-1 = 1

高さが2であれば、次のように3つのノードを持つ木になる。
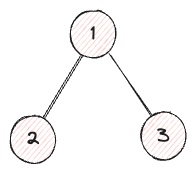
問題解決
まず中間順の結果を見てみよう。
問題で与えられた木は次のようであり、
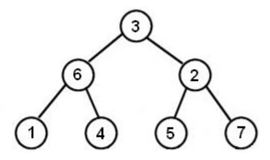
この木を中間順に巡った結果の例入力は[1, 6, 4, 3, 5, 2, 7]である。
配列を見れば、配列自体が何か木のように見えることがわかるが、
次のような配列を、

高さを少しずつ変えてみると?
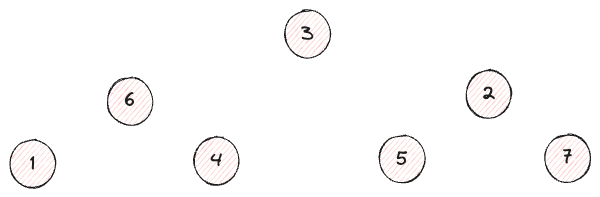
何か見え始める。
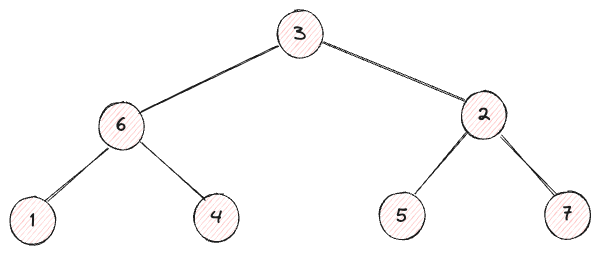
私たちが作りたい木の姿をそのまま捉えていることがわかる。
それでは、これをコードの形に変えてみよう。
この問題は高さごとのノードを出力することが目的なので、まずルートノードを見つける必要がある。
1. ルートノードを探す
完全二分木のルートノードは非常に簡単に見つけることができる。 先ほど述べたように、常に長さは2^h-1であり、先ほど述べたように中間順の木の形自体が木の形を平らに押しつぶした形になっているので、ルートノードは常に中央に位置する。
次の配列[1, 6, 4, 3, 5, 2, 7]で中央にある要素は3であり、先ほどの図で確認した通りルートノードであることがわかる。
コードで表現すると次のようになる。
root := arr[len(arr/2)]2. 子ノードを探す
子ノードはルートノードのインデックスを基準に左と右に分けて探すことができる。
中間順の配列を一度見てみよう。
[1, 6, 4, 3, 5, 2, 7]でルートノードの子はそれぞれ6番と2である。
それぞれのノードはルートノード3から2つのインデックスの差があることがわかる。
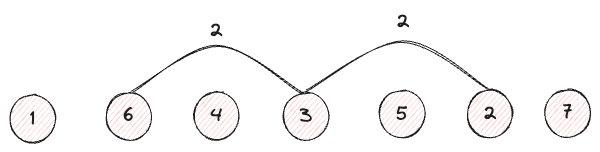
では、子の子を見てみよう。6と2の子はそれぞれ1,4と5,7である。
これらはそれぞれ6と2から1つのインデックスの差があることがわかる。
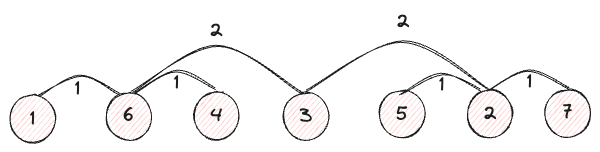
このように親から離れるにつれてインデックスの差が減少していくことがわかる。 ただし、どのような規則で遠ざかるのかはまだ確認しにくいので、他のノードをもう少し追加して見てみよう。
次のように理解を簡単にするために、中間順の結果が連続する数字になっていると仮定しよう。

ルートノードは真ん中の8であり、彼の子はそれぞれ4,12である。
それぞれのインデックスの差は4であることがわかる。

4と12の子を見てみよう。4の子は2,6であり、12の子は10,14である。
それぞれのインデックスの差は2であることがわかる。

残りは2と6の子はそれぞれ1,3と5,7であり、10と14はそれぞれ9,11と13,15である。 それぞれのインデックスの差は1であることがわかる。
このようにインデックスが差がある値は、高さによって高さ1のルートでは4、高さ2では2、高さ3では1であることがわかる。
これを式で表すと、全体の木の高さKに対して知りたい高さhのインデックスの差は次のようになる。
interval = 2^(K-h)設計
それでは1,2を総合してみよう。
まず(a)ルートノードを探し、(b)ルートを介してintervalだけ離れている子ノードを探し、(c)その子ノードを利用して、その子ノードの子に対してもintervalだけ離れているノードを探せば良いだろう。
答え
説明をコード部分に分けると関連する部分が多いため、コードの内注釈で代用することにする。
package main
import (
"bufio"
"fmt"
"log"
"os"
)
func main() {
writer := bufio.NewWriter(os.Stdout)
reader := bufio.NewReader(os.Stdin)
defer writer.Flush()
// 木の高さを入力を受け取る。
var K int
if _, err := fmt.Fscanln(reader, &K); err != nil {
log.Fatal(err)
}
// 木の高さを通じて木の長さを求め、中間順の配列を入力を受け取る。
length := 1<<K - 1
inOrder := make([]int, length)
for i := 0; i < length; i++ {
if _, err := fmt.Fscan(reader, &inOrder[i]); err != nil {
log.Fatal(err)
}
}
// ルートノードの初期インデックス: 全体の長さ / 2はルートノードである。
idxs := []int{length / 2}
// 高さhに応じた子ノードのインデックスを求める過程(最後の高さは子がないので、当ステップではidxsにだけ保存)
for h := 1; h < K; h++ {
children := make([]int, 0, 1<<(h))
interval := 1 << (K - h - 1)
for _, idx := range idxs {
_, _ = fmt.Fprint(writer, inOrder[idx], " ") // 高さhに対応する子ノードを出力
children = append(children, idx-interval, idx+interval) // 子ノードインデックスの保存
}
idxs = children
_, _ = fmt.Fprintln(writer)
}
// 最後の高さの子ノードを出力
for _, idx := range idxs {
_, _ = fmt.Fprint(writer, inOrder[idx], " ")
}
}結果

終わり
このように完全二分木の問題を解決することができた。この解決方法は他の人の解法を見て参照したものであるが、筆者の場合、最初はダミーインデックス木を作成して中間順を巡回した後、該当インデックスを利用して既存の木を推論する方式で進めていた。
しかし、その方式がコード自体が少しさらりしていて、すっきりしていると感じたため、この方式を借用した。
YangTaeyoung/algorithmで筆者が作成したこの問題に関するGoで書かれたアルゴリズム問題解法コードを見ることができる。