[BOJ-2579] 階段登り問題と動的プログラミング (Golang)
はじめに
実際に動的プログラミングをずっとやっていなかったためか、昔にやったときもただそういうものがあるんだなという程度で終わってしまったことが問題だったのか、今回の問題には手を付けられなかった。
そのため、今回は動的プログラミングをしっかり勉強しようと心に決めて、問題を解いてみた。
動的プログラミング(Dynamic Programming)とは?
動的プログラミング(Dynamic Programming、DP)は、問題を小さなサブ問題に分けて解決するアルゴリズム設計手法である。この手法は主に最適化問題に使用され、重複するサブ問題を効率的に解決するためにメモ化(Memoization)またはテーブルを使用して以前の計算結果を保存・再利用する形で動作する。
動的プログラミングは以下の2つの主な特性を持つ:
- 最適部分構造(Optimal Substructure):問題の最適な解決方法はサブ問題の最適な解決方法で構成できる。
- 重複するサブ問題(Overlapping Subproblems):同じサブ問題が複数回計算されることがある。
代表的な例としてフィボナッチ数列(Fibonacci Sequence)の計算がある。フィボナッチ数列は以下のような再帰式を持つ。
$$f(n) = f(n - 1) + f(n - 2)$$
解く方法はトップダウン方式とボトムアップ方式がある。トップダウン方式は再帰を使用してサブ問題を解決し、ボトムアップ方式は繰り返しを使用してサブ問題を解決するという点が異なる。
フィボナッチ数列を求める動的プログラミングを使ったコードは以下の通りである。
トップダウン方式 (Top-Down Approach)
package main
import "fmt"
var memo = make(map[int]int)
func fibonacci(n int,) int {
if n <= 1 {
return n
}
if val, exists := memo[n]; exists {
return val
}
memo[n] = fibonacci(n-1) + fibonacci(n-2)
return memo[n]
}
func main() {
n := 10
result := fibonacci(n)
fmt.Println("Fibonacci(", n, ") =", result)
}
}ボトムアップ方式 (Bottom-Up Approach)
package main
import "fmt"
func fibonacci(n int) int {
if n <= 1 {
return n
}
fib := make([]int, n+1)
fib[0], fib[1] = 0, 1
for i := 2; i <= n; i++ {
fib[i] = fib[i-1] + fib[i-2]
}
return fib[n]
}
func main() {
n := 10
result := fibonacci(n)
fmt.Println("Fibonacci(", n, ") =", result)
}
}核心ロジックを見ると、トップダウン方式は再帰とメモ化テーブルmemoを使用して重複するサブ問題を解決し、ボトムアップ方式は繰り返しを使用してサブ問題を解決している。
メモ化を使わないと?
実際、メモ化を使わなくても問題を解決するには問題ない。ただ、動的プログラミングに該当する問題は常に重複するサブ問題が存在するため、メモ化を使用しない場合、時間計算量が指数関数的に増加することになる。
例えば、フィボナッチ数列の特定の値である$f(5)$を求めるにはどうすればよいだろうか?
次のように式で表すことができる。 $$f(5) = f(4) + f(3)$$
そしてf(4)を求めるためには次のように表される。
$$f(4) = f(3) + f(2)$$
今、2つの式を見てみよう。注目すべき部分は$f(3)$である。$f(3)$は$f(4)$と$f(5)$を求めるために2回呼び出されている。
フィボナッチ数列では重複回数が最大で2回に制限されているが、他の動的プログラミングでは場合によっては重複回数が指数関数的に増加する可能性がある。
このようなことを参考にして次の問題である階段登り問題を解いてみよう。
問題
階段登りゲームは、階段の下のスタート地点から階段の上に位置するゴール地点まで行くゲームである。<図1>のようにそれぞれの階段には一定の点数が書かれており、階段を踏むとその階段に書かれている点数を得ることができる。
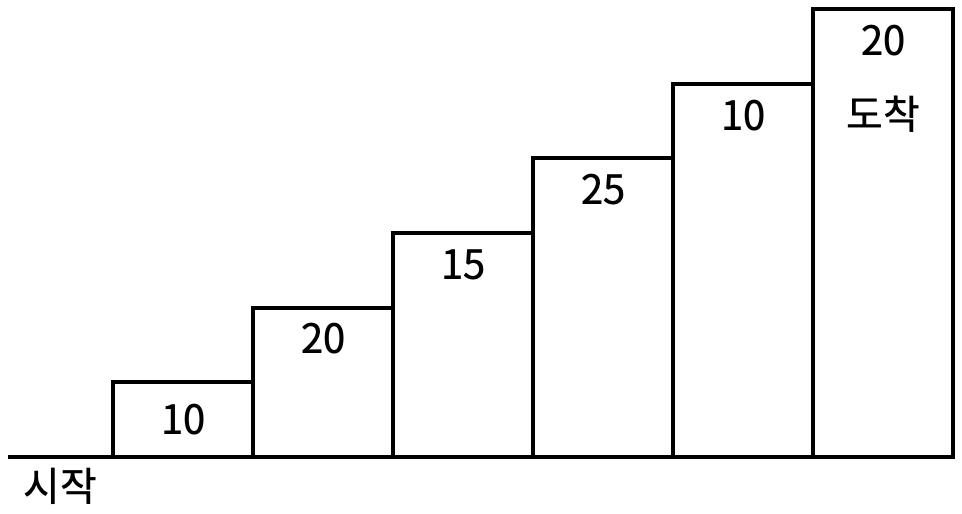
<図1>
例えば<図2>のようにスタート地点から最初の2番目、4番目、6番目の階段を踏み、ゴール地点に到達すると合計点は10 + 20 + 25 + 20 = 75点となる。
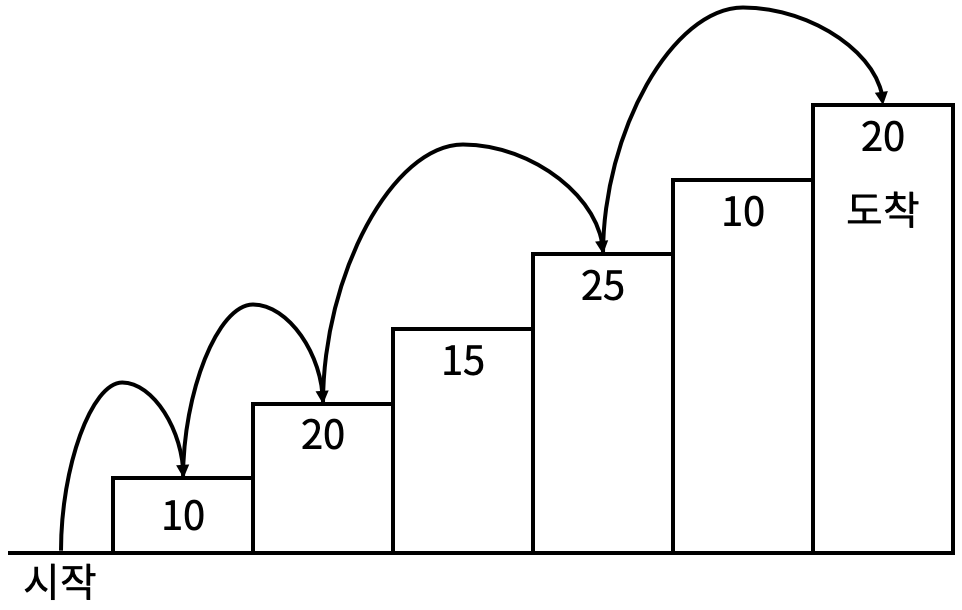
<図2>
階段を登るには以下のような規則がある。
階段は一度に1階段または2階段登ることができる。つまり、1階段を踏みながら次の階段または次の次の階段に登ることができる。 連続した3つの階段をすべて踏んではいけない。ただし、スタート地点は階段に含まれない。 最後の到達階段は必ず踏まなければならない。 したがって最初の階段を踏んで2番目の階段か、3番目の階段に登ることができる。しかし、最初の階段を踏んでそのまま4番目の階段に上がったり、最初の階段、2番目の階段、3番目の階段を連続してすべて踏むことはできない。
各階段に書かれている点数が与えられたとき、このゲームで得られる合計点数の最大値を求めるプログラムを作成しなさい。
アプローチ
問題をざっと読んだときはただ階段を全部登ればいいのかと思ったが、階段を登る規則を見てみると、連続した3つの階段を踏んではいけないという点が問題の核心である。
したがって、階段を登る方法は次のように大きく2つに分けることができる。
- 現在の階段を踏み前の階段を踏まず、その前の階段を踏む場合
- 現在の階段を踏み、前の階段も踏む場合
この2つのケースを全て考慮して最大値を求めなければならない。
まずn番目の階段での点数最大値をどうやって求めることができるだろうか?
上のケースを考えてみると2つのケースで表現できる。
ケース1: n番目の階段の点数 + (n-2)番目までの階段の点数最大値

ケース2: n番目の階段の点数 + (n-1)番目の階段の点数 + (n-3)番目までの階段の点数最大値

ケース2で単に$n-1$番目までの最大値を指定していない理由は、$n-1$番目の階段を踏んだ場合、$n-2$番目の階段を踏まなかったことが確定するためである。
再帰式
これをそれぞれの再帰式で表すと次のようになる。
$$f(n) = ext{max}(f(n-2) + s(n), f(n-3) + s(n-1) + s(n))$$
ここで$f(n)$はn番目の階段での最大値、$s(n)$はn番目の階段の点数を意味する。
初期値指定は再帰式にある$f()$内の数値が持つことができる最小値をそれぞれ指定してあげなければならない。
つまり、該当再帰式で関数内部にある数字はそれぞれ$n-1$、$n-2$、$n-3$に該当するため、初期値はインデックスの最小値0、1、2に対して次のように指定される必要がある。
これに従って全体の再帰式を整理すると次のようになる。
$$f(0) = s(0)$$ $$f(1) = s(0) + s(1)$$ $$f(2) = ext{max}(s(0) + s(2), s(1) + s(2))$$ $$f(n) = ext{max}(f(n-2) + s(n), f(n-3) + s(n-1) + s(n))$$
コード
再帰式が出たので、コードを書くのはさほど難しくない。
これに従って全体のコードを記述すると次のようになる。
package main
import (
"bufio"
"fmt"
"log"
"os"
)
var memo = make(map[int]int)
func dp(stairs []int, n int) int {
if value, ok := memo[n]; ok {
return value
}
if n == 0 {
return stairs[0]
}
if n == 1 {
return stairs[0] + stairs[1]
}
if n == 2 {
return max(stairs[0]+stairs[2], stairs[1]+stairs[2])
}
// 二階段を一度に
case1 := dp(stairs, n-2) + stairs[n]
// 1段ずつ二回登る場合
case2 := dp(stairs, n-3) + stairs[n-1] + stairs[n]
memo[n] = max(case1, case2)
return memo[n]
}
func main() {
writer := bufio.NewWriter(os.Stdout)
reader := bufio.NewReader(os.Stdin)
defer writer.Flush()
var N int
if _, err := fmt.Fscan(reader, &N); err != nil {
log.Fatal(err)
}
stairs := make([]int, N)
for i := 0; i < N; i++ {
if _, err := fmt.Fscan(reader, &stairs[i]); err != nil {
log.Fatal(err)
}
}
fmt.Fprintln(writer, dp(stairs, N-1))
}