[Programmers] Joystick (Golang)

26 mai 2025

Problème

Complétez le nom alphabetique avec le joystick. Au départ, il est composé uniquement de A.
ex) Si le nom à compléter fait trois lettres, c'est AAA, si quatre lettres, c'est AAAA.

En déplaçant le joystick dans chaque direction, cela se présente comme suit :

▲ - Lettre suivante
▼ - Lettre précédente (en déplaçant vers le bas depuis A, on arrive à Z)
◀ - Déplacer le curseur à gauche (si on est au premier caractère et qu'on déplace à gauche, le curseur ira au dernier caractère)
▶ - Déplacer le curseur à droite (si on est au dernier caractère et qu'on déplace à droite, le curseur ira au premier caractère)
Par exemple, on peut obtenir "JAZ" de la manière suivante :

- À partir de la première position, manipulez le joystick vers le haut 9 fois pour compléter J.
- Déplacez le joystick à gauche 1 fois pour amener le curseur à la dernière position.
- À la dernière position, manipulez le joystick vers le bas 1 fois pour compléter Z.
Ainsi, il est possible de créer "JAZ" avec 11 mouvements, ce qui est le minimum.
Lorsque le nom que l'on veut créer, name, est donné comme paramètre, créez une fonction solution qui retourne le nombre minimum de manipulations du joystick pour ce nom.

Ce problème est classé dans la partie pratique des tests de programmation sous le niveau 2, mais je trouve personnellement que c’est un problème plus difficile qu’il n’y paraît.

~~Pour moi, c’était plutôt un niveau 3.~~

Approche

Ce problème peut être divisé en deux grandes parties :

Compléter les lettres avec le joystick en déplaçant vers le haut/bas.
Déplacer le curseur en utilisant le joystick à gauche/droite.

La première partie est plus simple qu’on ne le pense, mais la deuxième est plus complexe.

1. Compléter les lettres avec le joystick en déplaçant vers le haut/bas

Le processus de compléter les lettres avec le joystick en le déplaçant vers le haut/bas est plus simple qu’on ne le pense. On peut approcher le problème en considérant les deux directions et en trouvant la valeur minimale.

package main

func min(arr ...int) int {
	value := arr[0]
	for _, n := range arr {
		if n < value {
			value = n
		}
	}
	return value
}

func solution(name string) int {
	verticalMove := 0
	for _, alpha := range name {
		asc := int(alpha - 'A')
		desc := int('Z' - alpha + 1)
		verticalMove += min(asc, desc)
	}
	
	// ... omis
}

La valeur initiale est remplie par des A équivalents à la longueur de la chaîne. Par conséquent, pour partir de A, si c’est A, cela devient 0, et si c’est B, cela devient 1. En utilisant les valeurs ASCII, on peut calculer simplement alpha-'A', où si alpha est A, cela équivaut à 0, si c’est B, cela équivaut à 1, si c’est C, alors c’est 2, ainsi cela satisfait les conditions.

La direction inverse peut être calculée par Z - alpha + 1. Par exemple, pour Z, si l’on fait seulement 'Z' - alpha, cela devient 0 puisque Z-Z serait égal à 0, mais comme on utilise un joystick, une manipulation est nécessaire, donc on ajoute 1.

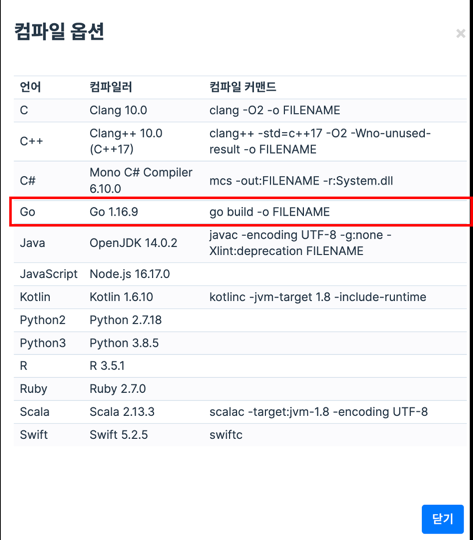
Ici, j’ai également défini une fonction min. En fait, la fonction min est une fonction intégrée standard en Go, mais Programmers utilise une version très ancienne de Go, 1.16.9, donc je devais la définir moi-même.

À titre de référence, la fonction min est fournie à partir de Go version 1.21 en tant que fonction intégrée standard.

2. Déplacer le curseur avec le joystick à gauche/droite

J’ai eu plus de mal avec cette partie que prévu.

~~C’est pourquoi j’ai demandé de l’aide à ChatGPT, et c’est pour cela que je rédige ce poste de réflexion.~~

Le problème réside dans l’existence de A consécutifs, et comme le problème stipule que l’on remplit automatiquement avec des A, le nombre minimum de mouvements du joystick requis pour déplacer le curseur peut varier selon la direction du mouvement.

Exemple de cas : `AAAA`

Imaginons que nous écrivons le nom AAAA. Dans ce cas, il n’est pas nécessaire d’écrire le nom, car il est déjà rempli de A.

Exemple de cas : `AABA`

Imaginons que nous écrivons le nom AABA.
Dans ce cas, il existe des méthodes pour se déplacer de gauche à droite et de droite à gauche.

Dans le mouvement à gauche, jusqu’à AA, tout est déjà complété, donc il suffira de déplacer le curseur 2 fois vers la droite et de changer la lettre une fois pour compléter AABA. Cela nécessitera un total de 3 manipulations.

Dans le mouvement à droite, pour compléter AABA, il faudra déplacer le curseur 1 fois vers la gauche, puis changer la lettre une fois pour compléter AABA. Cela nécessitera un total de 2 manipulations.

C’est une simple illustration, mais nous pouvons envisager des exemples plus complexes.

Exemple de cas : `BBBAAAAAAAAAB`

Regardons par exemple un nom BBBAAAAAAAAAB. Si l’on fait juste un passage vers la droite comme avant, cela nécessitera ▲ 2 fois, ▶ 11 fois, ▲ 1 fois, donc un total de 14 manipulations.

Si l’on fait juste un passage vers la gauche, cela nécessitera ▲ 2 fois, ◀ 11 fois, ▲ 1 fois, donc un total de 14 manipulations.

Cependant, et si l’on s’arrête juste après avoir écrit BBB?
Ici, pour changer B, cela nécessitera ▲ 3 fois pour le curseur, puis ▶ 2 fois pour aller, et revenir à la dernière position avec ◀ 3 fois, et changer la dernière B nécessitera ▲ 1 manipulation pour un total de 9 manipulations.

Et que se passe-t-il si l’on déplace cela vers l’arrière en premier?
Dans ce cas, pour amener le curseur à la dernière B, cela nécessitera ◀ 1 fois, changer B nécessitera ▲ 1 fois, déplacer à droite nécessitera ▶ 1 fois, changer la lettre nécessitera ▲ 3 fois, et aller vers la droite nécessitera ▶ 2 fois, ce qui implique un total de 8 manipulations.

Ainsi, les mouvements à gauche/droite du joystick peuvent avoir un nombre minimum variable en fonction des A consécutifs et de la position.

Donc, pour résoudre ce problème, chaque fois que l’on déplace le curseur, nous devrons envisager les méthodes pour se déplacer jusqu’à la prochaine A et vice versa, afin de trouver la valeur minimale avec un algorithme glouton.

Code

Examinons d’abord le code\n```go package main

func solution(name string) int { // … omis horizontalMove := len(name) - 1 for i := 0; i < len(name)-1; i++ { next := i + 1 for next < len(name) && name[next] == ‘A’ { next++ } // Déplacement à droite, puis retour vers la gauche moveRightLeft := (i * 2) + (len(name) - next) // Déplacement à gauche, puis retour vers la droite moveLeftRight := (len(name)-next)*2 + i

	horizontalMove = min(horizontalMove, moveRightLeft, moveLeftRight)
}
// ... omis

}


Tout d'abord, la valeur maximale de `horizontalMove` est `len(name) - 1`. Cela signifie déplacer le curseur du début à la fin sans changer de direction.
```go
horizontalMove := len(name) - 1

Ensuite, nous déclarons next. Lorsque next est A, nous déplacerons le curseur jusqu’à la fin de A, pour ensuite calculer le nombre minimum de mouvements du curseur en utilisant la différence entre next et i.

next := i + 1
for next < len(name) && name[next] == 'A' {
	next++
}

Ensuite, les valeurs moveRightLeft et moveLeftRight sont calculées.

// Déplacement à droite, puis retour vers la gauche
moveRightLeft := (i * 2) + (len(name) - next)
// Déplacement à gauche, puis retour vers la droite
moveLeftRight := (len(name)-next)*2 + i

Comme son nom l’indique, moveRightLeft signifie qu’après un déplacement vers la droite de i, on revient i vers la gauche, puis on déplace len(name) - next vers la gauche.

Une illustration ci-dessous peut aider à mieux comprendre.

Dans l’image, 1 et 2 représentent le déplacement de i, et 3 représente le déplacement de len(name) - next.

D’autre part, moveLeftRight signifie qu’on se déplace vers la gauche de len(name) - next, puis revient sur len(name) - next, et se déplace de i vers la droite.

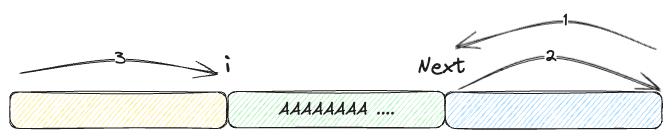
Dans l’image, 1 et 2 représentent le déplacement de len(name) - next, et 3 représente un mouvement vers la droite de i.

Par conséquent, l’algorithme ci-dessus pour calculer horizontalMove peut être considéré comme une méthode pour trouver la valeur minimale parmi plusieurs cas.

Mouvement unidirectionnel uniquement : len(name) - 1
Depuis chaque index i, se déplacer à droite puis à gauche : (i * 2) + (len(name) - next)
Depuis chaque index i, se déplacer à gauche puis à droite : (len(name)-next)*2 + i

Avec cela, nous pouvons finalement déterminer la valeur minimum des manipulations du joystick pour tous les index concernant name.

Code Final

package main

import "fmt"

func min(arr ...int) int {
	value := arr[0]
	for _, n := range arr {
		if n < value {
			value = n
		}
	}
	return value
}

func solution(name string) int {
	verticalMove := 0
	for _, alpha := range name {
		asc := int(alpha - 'A')
		desc := int('Z' - alpha + 1)
		verticalMove += min(asc, desc)
	}

	horizontalMove := len(name) - 1
	for i := 0; i < len(name)-1; i++ {
		next := i + 1
		for next < len(name) && name[next] == 'A' {
			next++
		}
		// Déplacement à droite, puis retour vers la gauche
		moveRightLeft := (i * 2) + (len(name) - next)
		// Déplacement à gauche, puis retour vers la droite
		moveLeftRight := (len(name)-next)*2 + i

		horizontalMove = min(horizontalMove, moveRightLeft, moveLeftRight)
	}

	return verticalMove + horizontalMove
}

func main() {
	case1 := solution("JEROEN")
	fmt.Println(case1)
	case2 := solution("JAN")
	fmt.Println(case2)
}

[Programmers] Inspection d'entrée (Golang)[BOJ-2579] Problème de montée d'escaliers et programmation dynamique (Golang)