[BOJ-9934] Arbre binaire complet (Golang)
Aperçu
En préparant un changement de carrière, j’ai revisité les algorithmes d’arbre et j’ai décidé de rédiger ce post.
Le problème d’arbre binaire complet consiste à déterminer la forme d’un arbre binaire complet à partir d’un tableau représentant l’ordre d’un parcours infixe. Il est donc essentiel de comprendre le concept de parcours infixe.
Parcours infixe
Les notions de parcours préfixe, infixe et postfixe se basent sur la position du nœud.
Nœud -> sous-arbre gauche -> sous-arbre droit
Dans cet ordre, le nœud est en premier, donc c’est un parcours préfixe.
Si l’on considère l’ordre sous-arbre gauche -> nœud -> sous-arbre droit, alors le nœud est au milieu, donc c’est un parcours infixe.
Et enfin, si l’on suit l’ordre sous-arbre gauche -> sous-arbre droit -> nœud, alors le nœud est le dernier, ce qui donne un parcours postfixe.
Le mode que nous allons examiner est le parcours infixe, dont un exemple est présent dans l’image suivante.
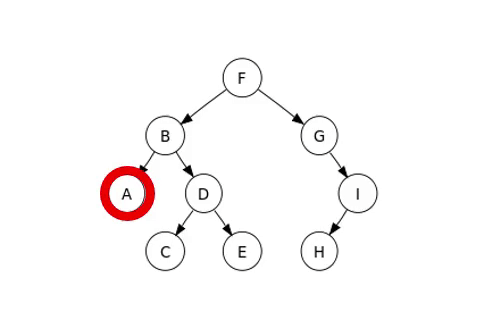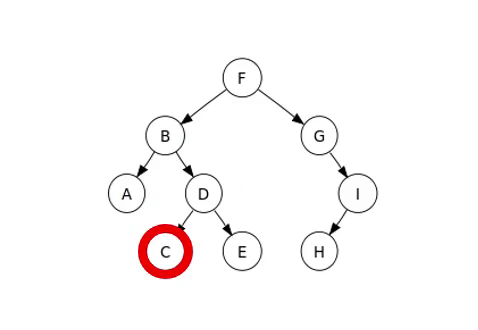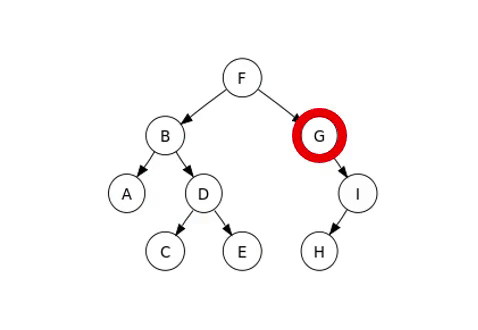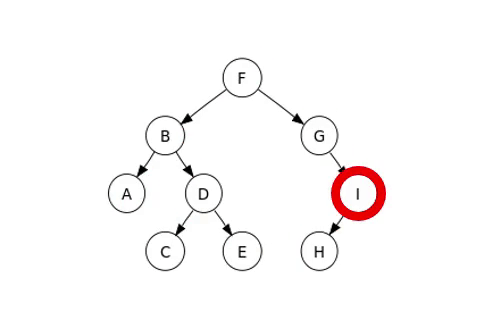
Arbre binaire complet
Un arbre binaire complet se définit par le fait que le nombre total de nœuds satisfait la condition 2^h-1 pour une hauteur d’arbre h donnée.
Un arbre binaire est un arbre dans lequel chaque nœud a au maximum 2 enfants.
En d’autres termes, il représente un arbre où tous les nœuds sont remplis jusqu’à la hauteur spécifiée.
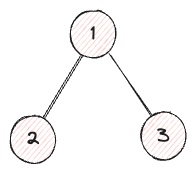
Par exemple, pour un arbre de hauteur 1, il n’y a qu’un seul nœud comme illustré ci-dessous.
Nombre de nœuds = 2^1-1 = 1

Pour une hauteur de 2, cela donne un arbre de 3 nœuds comme suit.
Résolution du problème
Pour commencer, observons le résultat du parcours infixe.
L’arbre donné dans le problème est le suivant,
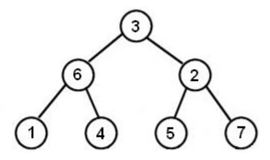
Un exemple d’entrée pour le résultat de ce parcours infixe est [1, 6, 4, 3, 5, 2, 7].
En regardant le tableau, on peut voir que le tableau lui-même ressemble à un arbre.
Prenons un tableau comme celui-ci,

En modifiant légèrement la hauteur ?
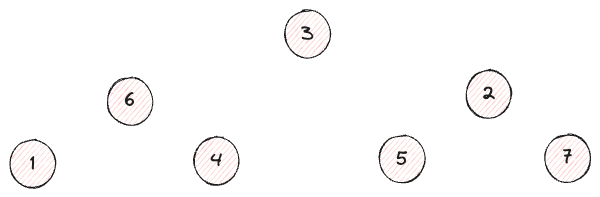
On commence à voir quelque chose.
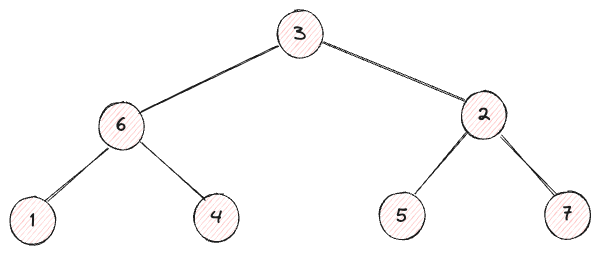
Nous pouvons constater qu’il reflète exactement la forme de l’arbre que nous cherchions à créer.
Transformons cela en code.
Le but de ce problème est d’imprimer les nœuds par hauteur, donc nous devons d’abord trouver le nœud racine.
1. Trouver la nœud racine
Il est très simple de trouver le nœud racine d’un arbre binaire complet. Comme mentionné précédemment, il a toujours une longueur de 2^h-1, et comme indiqué précédemment, la forme du arbre à partir du parcours infixe est comprimée, donc le nœud racine est toujours situé au centre.
Dans le tableau [1, 6, 4, 3, 5, 2, 7], l’élément central est 3, ce qui indique qu’il s’agit du nœud racine, comme nous l’avons vérifié dans l’image précédente.
En code, cela se traduit par :
root := arr[len(arr/2)]2. Trouver les nœuds enfants
Les nœuds enfants peuvent être divisés en gauche et droite selon l’indice du nœud racine.
Examinons à nouveau le tableau de parcours infixe.
Les enfants du nœud racine 3 sont 6 et 2 respectivement.
Nous pouvons constater que chaque nœud a un écart de 2 indices par rapport au nœud racine 3.
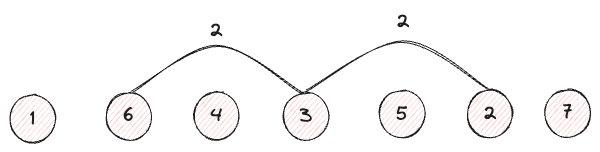
Examiner les enfants des enfants, 6 et 2 ont pour enfants respectivement 1, 4 et 5, 7.
Nous pouvons constater qu’ils sont chacun séparés de 1 indice.
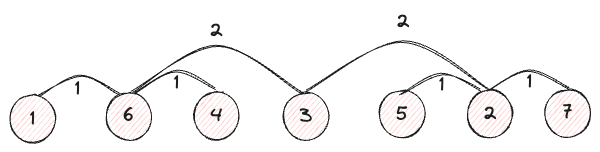
Ainsi, en s’éloignant du parent, on constate que l’écart d’indices diminue. Cependant, il est encore difficile de déterminer selon quelle règle cela s’éloigne, donc ajoutons d’autres nœuds pour examiner la situation.
Pour simplifier la compréhension, supposons que le résultat du parcours infixe contienne des nombres consécutifs.

Le nœud racine est le centrale 8, et ses enfants sont respectivement 4 et 12.
On peut constater que l’écart d’indices est 4.

Investigons les enfants de 4 et 12, 4 a 2 et 6, tandis que 12 a 10 et 14.
L’écart d’indices ici est 2.

En continuant, 2 et 6 ont respectivement 1 et 3, ainsi que 5 et 7, tandis que 10 et 14 ont respectivement 9 et 11, et 13 et 15. L’écart d’indices est 1 dans tous les cas.
Nous pouvons voir que l’écart d’indices change selon la hauteur, où pour la racine de hauteur 1, l’écart est 4, pour la hauteur 2, l’écart est 2, et pour la hauteur 3, l’écart est 1.
Nous pouvons exprimer cela arithmétiquement, pour une hauteur totale d’arbre K, l’écart d’indices d’une hauteur h donnée est:
interval = 2^(K-h)Design
Récapitulons les points (a), (b) et (c).
Tout d’abord, (a) trouvons le nœud racine, puis (b) trouvons les enfants séparés par interval à partir de la racine, puis (c) pour chaque nœud enfant, utilisons-le pour retrouver les nœuds enfants des enfants respectivement.
Solution
Il y a beaucoup de parties interconnectées, donc je vais les gérer via des commentaires dans le code.
package main
import (
"bufio"
"fmt"
"log"
"os"
)
func main() {
writer := bufio.NewWriter(os.Stdout)
reader := bufio.NewReader(os.Stdin)
defer writer.Flush()
// Obtention de la hauteur de l'arbre
var K int
if _, err := fmt.Fscanln(reader, &K); err != nil {
log.Fatal(err)
}
// Calculer la longueur de l'arbre en fonction de sa hauteur et obtenir le tableau de parcours infixe
length := 1<<K - 1
inOrder := make([]int, length)
for i := 0; i < length; i++ {
if _, err := fmt.Fscan(reader, &inOrder[i]); err != nil {
log.Fatal(err)
}
}
// Indice initial du nœud racine : longueur totale / 2
idxs := []int{length / 2}
// Processus pour obtenir l'indice des nœuds enfants en fonction de la hauteur h
for h := 1; h < K; h++ {
children := make([]int, 0, 1<<(h))
interval := 1 << (K - h - 1)
for _, idx := range idxs {
_, _ = fmt.Fprint(writer, inOrder[idx], " ") // Impression des nœuds enfants pour la hauteur h
children = append(children, idx-interval, idx+interval) // Enregistrement des indices des nœuds enfants
}
idxs = children
_, _ = fmt.Fprintln(writer)
}
// Impression des nœuds enfants de la dernière hauteur
for _, idx := range idxs {
_, _ = fmt.Fprint(writer, inOrder[idx], " ")
}
}Résultat

Conclusion
Nous avons réussi à résoudre le problème d’arbre binaire complet. Cette méthode de résolution a été inspirée par la solution d’une autre personne. Au début, j’avais en fait l’intention de créer un arbre d’indices fictifs et d’exécuter un parcours infixe, puis d’utiliser ces indices pour déduire l’arbre d’origine.
Cependant, j’ai trouvé que cette méthode était plus concise et plus propre, donc j’ai adopté cette approche.
Vous pouvez consulter le code de la solution de problème que j’ai rédigée en Go sur YangTaeyoung/algorithm.