[BOJ-2579] Problème de montée d'escaliers et programmation dynamique (Golang)
Introduction
En fait, je n’ai pas pratiqué la programmation dynamique depuis trop longtemps et, même quand je l’ai fait auparavant, je l’ai simplement traitée comme quelque chose d’existant sans vraiment m’y plonger. C’était peut-être cela le problème, car je n’avais jamais touché à ce sujet.
C’est pourquoi j’ai décidé d’étudier la programmation dynamique comme il se doit et de résoudre un problème.
Qu’est-ce que la programmation dynamique ?
La programmation dynamique (Dynamic Programming, DP) est une technique de conception d’algorithmes qui consiste à diviser un problème en sous-problèmes plus petits. Cette technique est généralement utilisée pour des problèmes d’optimisation et fonctionne en utilisant la mémoïsation (Memoization) ou des tableaux pour sauvegarder et réutiliser les résultats de calcul précédents afin de résoudre efficacement les sous-problèmes qui se chevauchent.
La programmation dynamique a deux propriétés principales :
- Structure optimale (Optimal Substructure) : La solution optimale du problème peut être constituée des solutions optimales des sous-problèmes.
- Sous-problèmes qui se chevauchent (Overlapping Subproblems) : Il est possible que le même sous-problème soit calculé plusieurs fois.
Un exemple classique de cette technique serait le calcul de la suite de Fibonacci. La suite de Fibonacci est régie par la relation de récurrence suivante :
$$f(n) = f(n - 1) + f(n - 2)$$
Il existe deux approches pour résoudre ce problème : la méthode top-down et la méthode bottom-up. La méthode top-down utilise la récursivité pour résoudre les sous-problèmes, tandis que la méthode bottom-up utilise des boucles pour le faire.
En utilisant la programmation dynamique pour calculer la suite de Fibonacci, cela pourrait être codé comme suit :
Méthode Top-Down
package main
import "fmt"
var memo = make(map[int]int)
func fibonacci(n int,) int {
if n <= 1 {
return n
}
if val, exists := memo[n]; exists {
return val
}
memo[n] = fibonacci(n-1) + fibonacci(n-2)
return memo[n]
}
func main() {
n := 10
result := fibonacci(n)
fmt.Println("Fibonacci(", n, ") =", result)
}Méthode Bottom-Up
package main
import "fmt"
func fibonacci(n int) int {
if n <= 1 {
return n
}
fib := make([]int, n+1)
fib[0], fib[1] = 0, 1
for i := 2; i <= n; i++ {
fib[i] = fib[i-1] + fib[i-2]
}
return fib[n]
}
func main() {
n := 10
result := fibonacci(n)
fmt.Println("Fibonacci(", n, ") =", result)
}En examinant la logique clé, on peut voir que la méthode top-down utilise la récursivité et le tableau de mémoïsation memo pour résoudre les sous-problèmes en double, tandis que la méthode bottom-up utilise des boucles pour le faire.
Que se passe-t-il si nous n’utilisons pas de mémoïsation ?
En fait, même sans mémoïsation, il n’y a pas de problème à résoudre le problème. Cependant, comme les problèmes relevant de la programmation dynamique présentent toujours des sous-problèmes qui se chevauchent, le temps de calcul devient exponentiellement élevé si la mémoïsation n’est pas utilisée.
Prenons un exemple.
Comment devrions-nous calculer une valeur spécifique de la suite de Fibonacci $f(5)$ ?
Cela peut être exprimé par l’équation suivante : $$f(5) = f(4) + f(3)$$
Et pour calculer f(4), cela peut être écrit comme ceci :
$$f(4) = f(3) + f(2)$$
Regardons maintenant ces deux équations. Ce qui mérite d’être noté est $f(3)$. $f(3)$ a été appelé deux fois pour résoudre $f(4)$ et $f(5)$.
Dans la suite de Fibonacci, le nombre maximum de doublons est limité à 2 fois, mais dans d’autres cas de programmation dynamique, le nombre de doublons peut augmenter de manière exponentielle selon les circonstances.
Prenant tout cela en considération, résolvons maintenant le problème suivant, le problème de montée d’escaliers.
Problème
Le jeu de montée d’escaliers commence à partir d’un point de départ en bas des escaliers jusqu’à atteindre le sommet des escaliers. Comme montré dans <Figure 1>, chaque marche a un score qui lui est attribué, et en marchant sur une marche, on acquiert le score inscrit sur celle-ci.
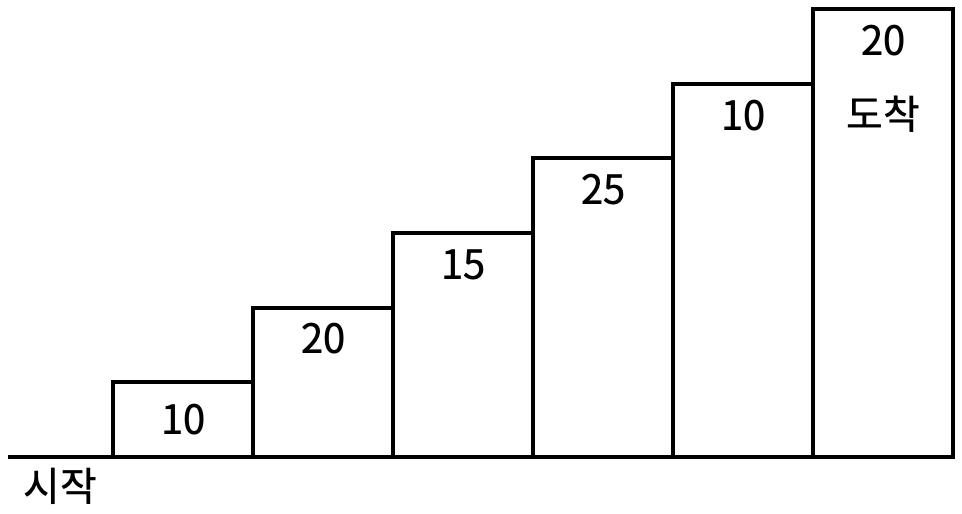
Par exemple, si l’on marche sur la première, la deuxième, la quatrième et la sixième marches comme illustré dans <Figure 2>, le score total sera de 10 + 20 + 25 + 20 = 75 points.
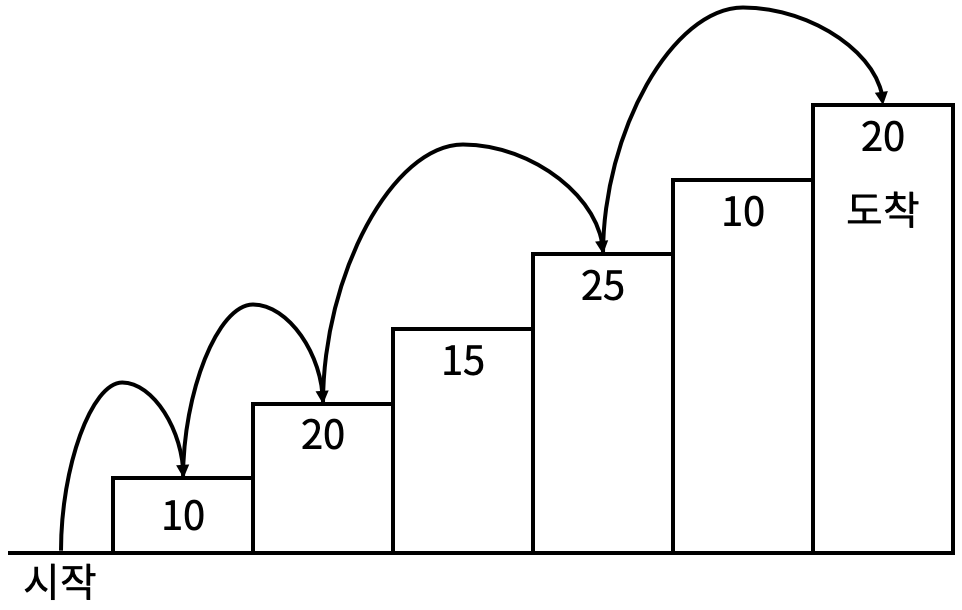
Il existe des règles pour monter les marches.
On peut monter une marche ou deux marches à la fois. C’est-à-dire qu’on peut avancer d’une marche et aller vers la suivante ou sa suivante suivante.
On ne peut pas marcher sur trois marches consécutives. Cependant, le point de départ n’est pas inclus dans les marches.
La dernière marche d’arrivée doit nécessairement être foulée.
Ainsi, après avoir monté la première marche, on peut passer à la deuxième ou à la troisième. Cependant, on ne peut pas monter directement de la première à la quatrième marche ou marcher sur les première, deuxième et troisième marches consécutivement.
Écrivez un programme pour trouver le score total maximum que l’on peut obtenir dans ce jeu en prenant en compte les points donnés sur chaque marche.
Approche
Quand je lis rapidement le problème, je me dis que je peux simplement monter toutes les marches, mais en considérant les règles de montée des escaliers, notamment qu’on ne doit pas marcher sur trois marches consécutives, cela constitue le cœur du problème.
Ainsi, les façons de monter les marches peuvent être divisées en deux catégories principales :
- Marcher sur la marche actuelle, ne pas marcher sur la marche précédente, mais marcher sur la marche avant la précédente.
- Marcher sur la marche actuelle et sur la marche précédente.
Nous devons considérer tous ces cas pour en déterminer le maximum.
Comment trouver le score maximum à la n-ième marche ?
En examinant les cas mentionnés ci-dessus, cela peut être exprimé sous deux formes.
Cas 1 : score de la n-ième marche + score maximum jusqu’à la (n-2)-ième marche

Cas 2 : score de la n-ième marche + score de la (n-1)-ième marche + score maximum jusqu’à la (n-3)-ième marche

La raison pour laquelle nous n’avons pas simplement spécifié jusqu’à la marche (n-1) pour le cas 2 est pour s’assurer que nous n’avons pas marché sur la marche (n-2) en montant la marche (n-1).
Relation de récurrence
Cela peut être représenté par la relation de récurrence suivante :
$$f(n) = ext{max}(f(n-2) + s(n), f(n-3) + s(n-1) + s(n))$$
Ici, $f(n)$ représente la valeur maximale à la n-ième marche, et $s(n)$ représente le score de la n-ième marche.
Les valeurs initiales doivent être définies avec les valeurs minimales possibles dans la fonction de récurrence $f()$ pour les nombres.
C’est-à-dire que les chiffres à l’intérieur de la fonction de récurrence se rapportent respectivement à $n-1$, $n-2$, $n-3$, donc les valeurs initiales doivent être définies comme suit pour les indices minimums, qui sont 0, 1 et 2.
Pour résumer l’ensemble de la relation de récurrence, on obtient alors :
$$f(0) = s(0)$$ $$f(1) = s(0) + s(1)$$ $$f(2) = ext{max}(s(0) + s(2), s(1) + s(2))$$ $$f(n) = ext{max}(f(n-2) + s(n), f(n-3) + s(n-1) + s(n))$$
Code
Une fois que nous avons établi la relation de récurrence, écrire le code ne devrait pas être trop difficile.
En suivant cela, nous pouvons élaborer le code complet comme suit :
package main
import (
"bufio"
"fmt"
"log"
"os"
)
var memo = make(map[int]int)
func dp(stairs []int, n int) int {
if value, ok := memo[n]; ok {
return value
}
if n == 0 {
return stairs[0]
}
if n == 1 {
return stairs[0] + stairs[1]
}
if n == 2 {
return max(stairs[0]+stairs[2], stairs[1]+stairs[2])
}
// Deux marches à la fois
case1 := dp(stairs, n-2) + stairs[n]
// Montée d'une marche à la fois deux fois
case2 := dp(stairs, n-3) + stairs[n-1] + stairs[n]
memo[n] = max(case1, case2)
return memo[n]
}
func main() {
writer := bufio.NewWriter(os.Stdout)
reader := bufio.NewReader(os.Stdin)
defer writer.Flush()
var N int
if _, err := fmt.Fscan(reader, &N); err != nil {
log.Fatal(err)
}
stairs := make([]int, N)
for i := 0; i < N; i++ {
if _, err := fmt.Fscan(reader, &stairs[i]); err != nil {
log.Fatal(err)
}
}
fmt.Fprintln(writer, dp(stairs, N-1))
}