[Programmers] Joystick (Golang)

Problem

Programmers - Joystick

Complete the alphabet name using the joystick. Initially, it consists only of A.
For example, if the name to be completed has three letters, it is AAA. If it has four letters, it is AAAA.

Moving the joystick in each direction works as follows:

▲ - Next alphabet
▼ - Previous alphabet (Moving down from A goes to Z)
◀ - Move cursor left (If moving left from the first position, the cursor goes to the last character)
▶ - Move cursor right (If moving right from the last position, the cursor goes to the first character)
For example, "JAZ" can be created in the following way:

- Move the joystick up 9 times from the first position to complete J.
- Move the joystick left 1 time to position the cursor at the last character.
- Move the joystick down 1 time from the last position to complete Z.
Therefore, it is possible to create "JAZ" with 11 moves, and this is the minimum movement.
Create a solution function that returns the minimum number of joystick operations for the name provided as a parameter.

This problem is classified as LEVEL 2 in the coding test practice section, but honestly, it felt more challenging for me than expected.

For me, it felt like LEVEL 3.

Approach

This problem can be divided into two main parts.

1. Completing letters by moving the joystick up/down.
2. Moving the cursor left/right with the joystick.

The first part is easier than expected, but the second part is more difficult than I thought.

1. Completing letters by moving the joystick up/down.

Completing letters by moving the joystick up/down is actually quite simple. Consider both forward and backward sequences and approach it by finding the minimum and summing them up.

package main

func min(arr ...int) int {
	value := arr[0]
	for _, n := range arr {
		if n < value {
			value = n
		}
	}
	return value
}

func solution(name string) int {
	verticalMove := 0
	for _, alpha := range name {
		asc := int(alpha - 'A')
		desc := int('Z' - alpha + 1)
		verticalMove += min(asc, desc)
	}
	
	// ... omitted
}

The initial value is filled with A as long as the length of the string states. So, according to the forward sequence, if it is A, it becomes 0, and if B, it becomes 1. Using ASCII values, we can simply calculate it, so if alpha-'A', if the alpha value is A, it is 0, if B, it is 1, and if C, it is 2, which satisfies the condition.

The backward calculation can be done as Z - alpha + 1. For instance, in the case of Z, if we just did Z-alpha, it would yield Z-Z, which is 0, but since joystick adjustments are needed, we add 1 to it.

Here, I defined a min function additionally. In fact, the min function is also a built-in function in Go, but since Programmers uses a very old version 1.16.9, one has no choice but to define it manually.

For reference, the min function has been available as a standard built-in function since Go version 1.21.

2. Moving the cursor left/right with the joystick

In this part, I had more trouble than expected.

I got help from ChatGPT for this, which is why I am writing this reflective post.

The issue is the presence of consecutive As, which can change the minimum movement needed to move the cursor depending on the joystick adjustments due to the initial A filling in the problem conditions.

Example case: AAAA

Let’s say we are writing the name AAAA. In this case, there is no need to write the name. It is already filled with A.

Example case: AABA

Now let’s consider writing the name AABA. In this case, both ways exist: moving left to right, and vice versa.

For the left movement, since AA is already completed, only moving the cursor with ▶ 2 times followed by changing the alphabet to ▲ once can complete AABA. It requires a total of 3 joystick operations.

In the case of moving right, to complete AABA, the cursor must be moved 1 time to the left, and then ▲ once can complete AABA. A total of 2 joystick operations are needed.

This is a simple example, but more complex examples can also arise.

Example case: BBBAAAAAAAAAB

For instance, if we are writing the name BBBAAAAAAAAAB, like the previous example, if moving forward, we need ▲ 2 times, then ▶ 11 times, ▲ 1 time, which requires a total of 14 joystick operations.

If moving backward, we still need ▲ 2 times, then ◀ 11 times, ▲ 1 time, again a total of 14 joystick movements.

But what if we only enter up to BBB and then turn back? In this case, to change B, we will need ▲ 3 times, and to move the cursor in the forward direction will require ▶ 2 times, then go back to the last B with ◀ 3 times, and finally to change the last B with ▲ 1 time, for a total of 9 joystick operations.

What if we move backward first and then turn back? In this case, to go to the last B, it would require ◀ 1 time, then changing it to B would require ▲ 1 time, to move in the forward direction, it requires ▶ 1 time, and to change the B would require ▲ 3 times, and finally to move right would need ▶ 2, leading to a total of 8 joystick operations.

Consequently, the horizontal movement can change based on the cursor positioning and continuous A.

Thus, solving this part requires considering both ways of moving the cursor each time it goes to the next A and applying a greedy approach to find the minimum value.

Code

Let’s observe the code first and analyze it one by one.

package main

func solution(name string) int {
    // ... omitted
	horizontalMove := len(name) - 1
	for i := 0; i < len(name)-1; i++ {
		next := i + 1
		for next < len(name) && name[next] == 'A' {
			next++
		}
		// Move right then left to go left
		moveRightLeft := (i * 2) + (len(name) - next)
		// Move left then right to go right
		moveLeftRight := (len(name)-next)*2 + i

		horizontalMove = min(horizontalMove, moveRightLeft, moveLeftRight)
	}
	// ... omitted
}

Initially, the maximum value of horizontalMove is len(name) - 1, which means moving from the first position to the last position without changing direction.

horizontalMove := len(name) - 1

Next is to set the next variable considering each A. The loop stops when it reaches an A then moves to the next non-A character to check.

next := i + 1
for next < len(name) && name[next] == 'A' {
	next++
}

After that, we obtain moveRightLeft and moveLeftRight calculations.

// Move right then left to go left
moveRightLeft := (i * 2) + (len(name) - next)
// Move left then right to go right
moveLeftRight := (len(name)-next)*2 + i

As can be inferred from the names, moveRightLeft means moving right then returning left for indexed i and moving left as len(name) - next.

Looking at the diagram below should help clarify further.

In this image, 1 and 2 each signify moving i amount and 3 symbolizes moving by len(name) - next.

Meanwhile, moveLeftRight signifies moving left for len(name) - next, turn around for len(name) - next, finally moving right for i amount.

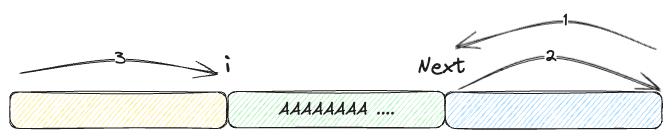
This diagram expresses that moving left is len(name) - next then returning len(name) - next before proceeding with a right move of i amount.

Thus, the overall algorithm finds the minimum move states for the joystick by considering:

1. The case of moving only in one direction: len(name) - 1
2. The scenario of right then left moving for each index i: (i * 2) + (len(name) - next)
3. The scenario of left then right moving for each index i: (len(name)-next)*2 + i

This ensures we gather the minimum joystick operation count across all indices regarding the name.

Final Code

package main

import "fmt"

func min(arr ...int) int {
	value := arr[0]
	for _, n := range arr {
		if n < value {
			value = n
		}
	}
	return value
}

func solution(name string) int {
	verticalMove := 0
	for _, alpha := range name {
		asc := int(alpha - 'A')
		desc := int('Z' - alpha + 1)
		verticalMove += min(asc, desc)
	}

	horizontalMove := len(name) - 1
	for i := 0; i < len(name)-1; i++ {
		next := i + 1
		for next < len(name) && name[next] == 'A' {
			next++
		}
		// Move right then left to go left
		moveRightLeft := (i * 2) + (len(name) - next)
		// Move left then right to go right
		moveLeftRight := (len(name)-next)*2 + i

		horizontalMove = min(horizontalMove, moveRightLeft, moveLeftRight)
	}

	return verticalMove + horizontalMove
}

func main() {
	case1 := solution("JEROEN")
	fmt.Println(case1)
	case2 := solution("JAN")
	fmt.Println(case2)
}