[BOJ-9934] Complete Binary Tree (Golang)
Overview
While preparing for a job change, I had the opportunity to study tree algorithms again after a long time, which led me to write this post.
The Complete Binary Tree Problem is a question where you need to determine and output the structure of a complete binary tree using an array obtained from an in-order traversal. To understand this problem, it is first necessary to grasp the concept of in-order traversal.
In-Order Traversal
The criteria for pre-order, in-order, and post-order traversals are determined by the position of the node.
If we traverse in the order of node -> left subtree -> right subtree, the node comes first, indicating pre-order traversal. Conversely, if we follow left subtree -> node -> right subtree, then the node is in the middle, representing in-order traversal.
Finally, if we traverse in the order of left subtree -> right subtree -> node, the node is last, thus indicating post-order traversal.
The traversal method we will examine is in-order traversal, with examples illustrated in the following image.
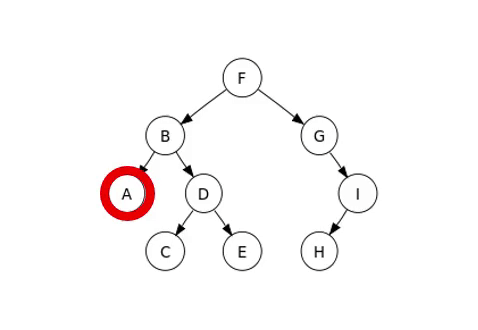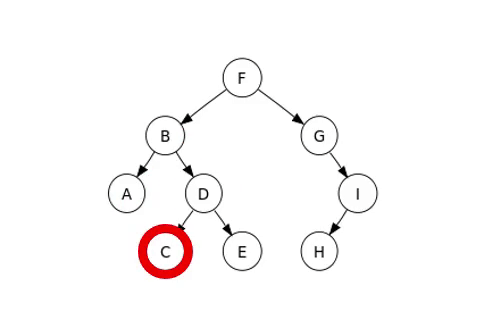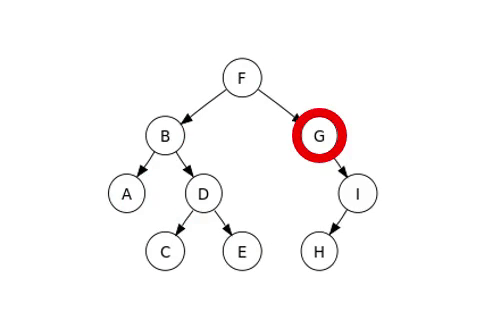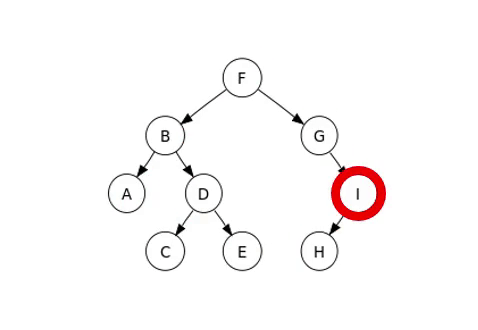
Complete Binary Tree
A complete binary tree is defined as a binary tree for which the total number of nodes satisfies 2^h - 1 for a given height h of the tree.
A binary tree is one where all nodes have at most 2 children.
In simpler terms, it refers to a tree where all nodes are fully filled up to a specified height.
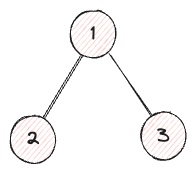
For example, if the height is 1, the tree simply has one node as shown below:
Number of nodes = 2^1 - 1 = 1

If the height is 2, the tree contains 3 nodes as follows:
Problem Solving
First, let’s examine the results of the in-order traversal.
The provided tree in the problem looks like this:
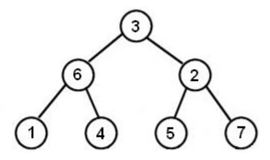
The example input for the result of the in-order traversal of this tree is [1, 6, 4, 3, 5, 2, 7].
From the array, we can see that it somewhat resembles a tree. By varying the height slightly,

patterns begin to emerge.
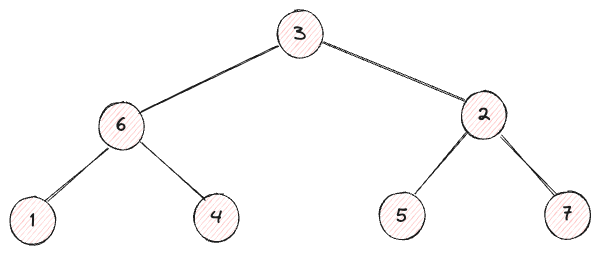
We can confirm that it encapsulates the shape of the tree we intend to build.
Now, let’s convert this into code.
Since the purpose of this problem is to output the nodes according to their heights, we first need to identify the root node.
1. Finding the Root Node
The root node of a complete binary tree can be located very simply. As mentioned earlier, it always has a length of 2^h - 1, and since in-order traversal flattens the tree’s shape, the root node is always positioned at the center.
In the array [1, 6, 4, 3, 5, 2, 7], the element in the center is 3, confirming it is the root node, as observed in the earlier figure.
In code, this can be expressed as follows:
root := arr[len(arr)/2]2. Finding Child Nodes
Child nodes can be identified by splitting according to the index of the root node, separating them into left and right children.
Let’s again look at the in-order traversal array.
In [1, 6, 4, 3, 5, 2, 7], the children of the root node are 6 and 2.
It is clear that each of those nodes has a difference of 2 indexes from the root node 3.
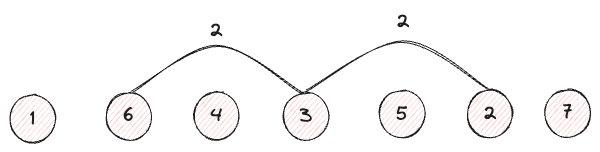
Now, examining the children of those children, 6 and 2 have children 1, 4 and 5, 7, respectively.
Each of them has a difference of 1 index from 6 and 2.
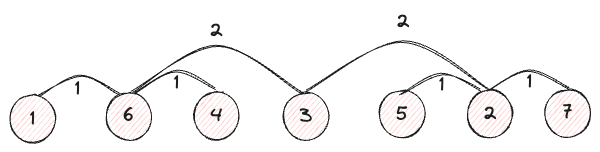
Thus, it is evident that as we move further away from the parent, the index differences decrease. However, the rule governing this distance is still unclear, so let’s add some more nodes to investigate.
To make it easier to understand, let’s assume the in-order traversal result consists of consecutive numbers.

The root node is in the middle at 8, while its children are 4 and 12.
The index differences here are clearly 4.

Now let’s look at the children of 4 and 12: children of 4 are 2, 6, while children of 12 are 10, 14.
Each of these has an index difference of 2.

The remaining nodes show that the children of 2 and 6 are 1, 3 and 5, 7, while 10 and 14 are 9, 11 and 13, 15 respectively. Each of these has an index difference of 1.
Thus, it can be concluded that the index differences are determined by the height: with a root at height 1 having a difference of 4, at height 2 the difference is 2, and at height 3 the difference is 1.
To express this in the form of a formula, the index difference for any height h within the total tree height K can be denoted as:
interval = 2^(K - h)Design
Let’s consolidate points (1) and (2).
First, (a) find the root node, (b) find the children positioned at an interval distance from the root, and (c) using that child node to find the grandchildren at the same interval distance.
Solution
Due to the interconnected nature of the explanations within the code, I’ll replace them with comments within the code itself.
package main
import (
"bufio"
"fmt"
"log"
"os"
)
func main() {
writer := bufio.NewWriter(os.Stdout)
reader := bufio.NewReader(os.Stdin)
defer writer.Flush()
// Get the height of the tree
var K int
if _, err := fmt.Fscanln(reader, &K); err != nil {
log.Fatal(err)
}
// Calculate tree length based on height, then accept in-order array as input
length := 1<<K - 1
inOrder := make([]int, length)
for i := 0; i < length; i++ {
if _, err := fmt.Fscan(reader, &inOrder[i]); err != nil {
log.Fatal(err)
}
}
// Initial index for the root node: total length / 2 is the root
idxs := []int{length / 2}
// Process to find child nodes based on height h (the last height has no children, so stored only in idxs)
for h := 1; h < K; h++ {
children := make([]int, 0, 1<<(h))
interval := 1 << (K - h - 1)
for _, idx := range idxs {
_, _ = fmt.Fprint(writer, inOrder[idx], " ") // Output child nodes for height h
children = append(children, idx-interval, idx+interval) // Save child node indices
}
idxs = children
_, _ = fmt.Fprintln(writer)
}
// Output child nodes for the last height
for _, idx := range idxs {
_, _ = fmt.Fprint(writer, inOrder[idx], " ")
}
}Result

Conclusion
Thus, we managed to solve the complete binary tree problem. I referenced this method from another person’s solution, where my initial approach was to create a dummy index tree, perform an in-order traversal, and then deduce the original tree using those indices.
However, this method seems more concise and cleaner, so I adopted it.
You can view the Go implementation of the algorithm problem I wrote on YangTaeyoung/algorithm.