[BOJ-2579] Climbing Stairs Problem and Dynamic Programming (Golang)
Introduction
In fact, the problem was that I hadn’t dealt with dynamic programming for too long, and even when I did, I just glossed over it, thinking, “Oh, this is a thing.” So I couldn’t even touch this problem.
This time, I decided to seriously study dynamic programming and attempted to solve the problem.
What is Dynamic Programming?
Dynamic Programming (DP) is an algorithm design technique that breaks a problem down into smaller subproblems and solves them. This technique is primarily used for optimization problems and operates by storing previous calculation results using memoization or tables, allowing for efficient solution of overlapping subproblems.
Dynamic programming has two main properties:
- Optimal Substructure: An optimal solution to the problem can be constructed from optimal solutions of its subproblems.
- Overlapping Subproblems: The same subproblem is solved multiple times.
A classic example is calculating the Fibonacci sequence. The Fibonacci sequence has the following recurrence relation:
$$f(n) = f(n - 1) + f(n - 2)$$
There are two ways to calculate it: a top-down approach and a bottom-up approach. The difference is that the top-down approach uses recursion to solve subproblems, while the bottom-up approach uses iterative methods.
Here is the representation of calculating the Fibonacci sequence using dynamic programming:
Top-Down Approach
package main
import "fmt"
var memo = make(map[int]int)
func fibonacci(n int,) int {
if n <= 1 {
return n
}
if val, exists := memo[n]; exists {
return val
}
memo[n] = fibonacci(n-1) + fibonacci(n-2)
return memo[n]
}
func main() {
n := 10
result := fibonacci(n)
fmt.Println("Fibonacci(", n, ") =", result)
}Bottom-Up Approach
package main
import "fmt"
func fibonacci(n int) int {
if n <= 1 {
return n
}
fib := make([]int, n+1)
fib[0], fib[1] = 0, 1
for i := 2; i <= n; i++ {
fib[i] = fib[i-1] + fib[i-2]
}
return fib[n]
}
func main() {
n := 10
result := fibonacci(n)
fmt.Println("Fibonacci(", n, ") =", result)
}Looking at the core logic, the top-down approach uses recursion and the memoization table memo to solve overlapping subproblems, whereas the bottom-up approach employs a loop to solve subproblems.
What if We Don’t Use Memoization?
In fact, it is possible to solve the problem without using memoization. However, since the problems targeted by dynamic programming always have overlapping subproblems, not using memoization would cause the time complexity to increase exponentially.
Let’s consider an example.
How can we compute a specific value of the Fibonacci sequence, say $f(5)$?
It can be expressed as follows: $$f(5) = f(4) + f(3)$$
To calculate f(4), it can be expressed as:
$$f(4) = f(3) + f(2)$$
Now, if we look at both equations, we notice that $f(3)$ has been called twice for calculating $f(4)$ and $f(5)$.
While the Fibonacci sequence is limited to a maximum of 2 overlapping calls, in other dynamic programming scenarios, the number of overlaps can increase exponentially.
With this in mind, let’s look at the next problem, the Climbing Stairs problem.
Problem
The climbing stairs game is played from the starting point at the bottom of the stairs to the endpoint at the top. As shown in <Figure 1>, each step has a certain score written on it, and you earn that score by stepping on the step.
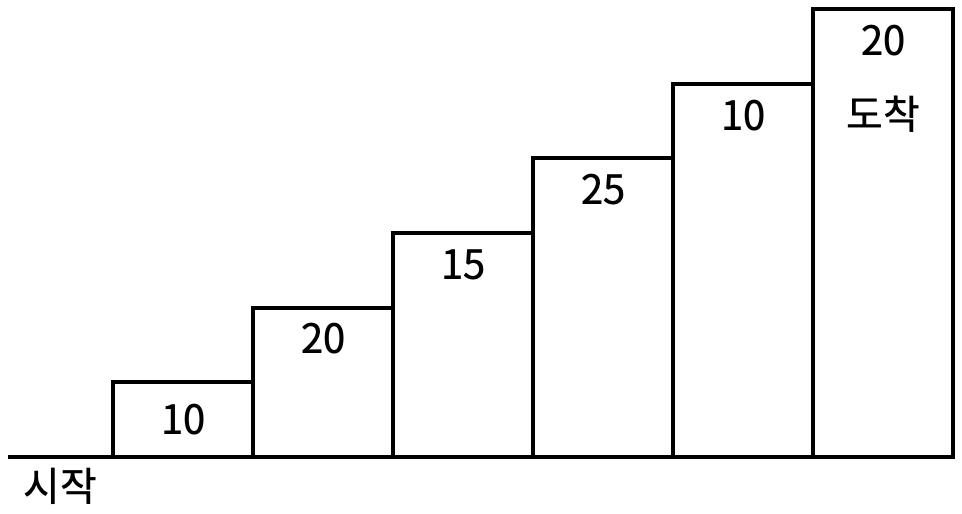
For example, if you step on the first, second, fourth, and sixth steps from the starting point to reach the endpoint, the total score would be 10 + 20 + 25 + 20 = 75 points.
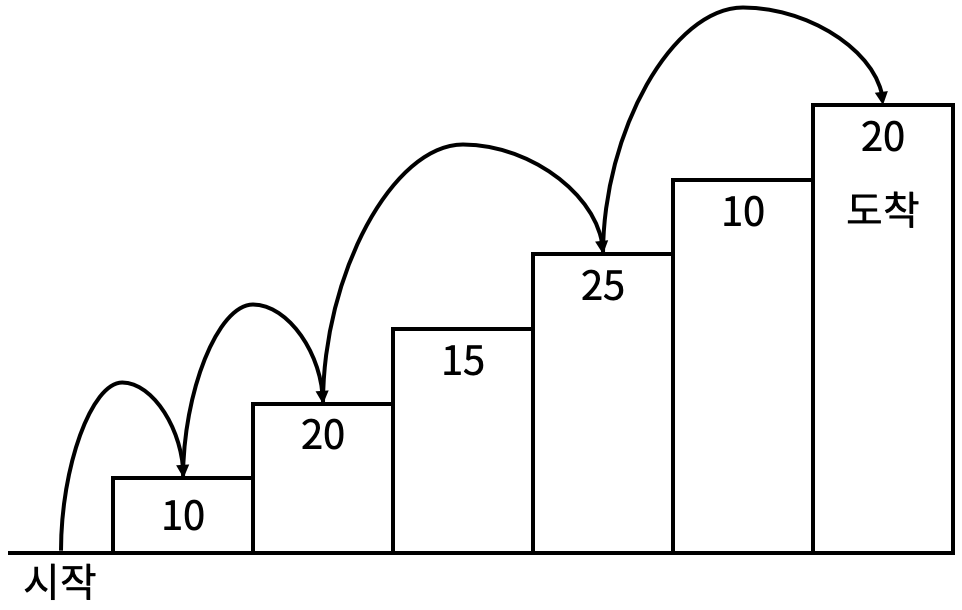
There are rules to climb the stairs:
You can climb either one step or two steps at a time. That is, you can go from one step to the next or jump to the step after next. You must not step on three consecutive stairs. The starting point is not included in the stair count. You must step on the last stair. Thus, from the first stair, you can step to the second or third stair, but you cannot jump from the first to the fourth or step consecutively on the first, second, and third stairs.
Given the scores written on each stair, write a program to find the maximum total score you can obtain in this game.
Approach
When I briefly read the problem, I thought, can’t we just climb all the stairs? However, looking at the rules for climbing the stairs, the key point is that you cannot step on three consecutive stairs.
Thus, there are essentially two main ways to approach climbing the stairs:
- Step on the current stair and skip the previous stair, then step on the stair before that.
- Step on the current stair and also step on the previous stair.
You need to consider both cases to obtain the maximum score.
How can we find the maximum score at the nth stair?
Considering the cases above, it can manifest in two forms:
Case 1: Score of the nth stair + Maximum score until the (n-2)th stair

Case 2: Score of the nth stair + Score of the (n-1)th stair + Maximum score until the (n-3)th stair

The reason the second case does not simply designate the maximum score up to the (n-1)th stair is to ensure that the (n-1)th stair was not stepped on when stepping on the (n-2)th stair.
Recurrence Relation
This can be expressed in the following recurrence relations:
$$f(n) = ext{max}(f(n-2) + s(n), f(n-3) + s(n-1) + s(n))$$
Where $f(n)$ represents the maximum score at the nth stair and $s(n)$ represents the score of the nth stair.
The initial values must be defined, specifying the minimum values that the numbers can take within the recurrence relation for $f()$.
Thus, the values inside the function at indices $n-1$, $n-2$, and $n-3$ must be specified as initial values for indices 0, 1, and 2.
The entire recurrence relation can then be organized as follows:
$$f(0) = s(0)$$ $$f(1) = s(0) + s(1)$$ $$f(2) = ext{max}(s(0) + s(2), s(1) + s(2))$$ $$f(n) = ext{max}(f(n-2) + s(n), f(n-3) + s(n-1) + s(n))$$
Code
Now that we have the recurrence relation, writing the code is not significantly difficult.
Following this, the entire code can be structured as follows:
package main
import (
"bufio"
"fmt"
"log"
"os"
)
var memo = make(map[int]int)
func dp(stairs []int, n int) int {
if value, ok := memo[n]; ok {
return value
}
if n == 0 {
return stairs[0]
}
if n == 1 {
return stairs[0] + stairs[1]
}
if n == 2 {
return max(stairs[0]+stairs[2], stairs[1]+stairs[2])
}
// Climbing two stairs at once
case1 := dp(stairs, n-2) + stairs[n]
// Climbing one stair twice
case2 := dp(stairs, n-3) + stairs[n-1] + stairs[n]
memo[n] = max(case1, case2)
return memo[n]
}
func main() {
writer := bufio.NewWriter(os.Stdout)
reader := bufio.NewReader(os.Stdin)
defer writer.Flush()
var N int
if _, err := fmt.Fscan(reader, &N); err != nil {
log.Fatal(err)
}
stairs := make([]int, N)
for i := 0; i < N; i++ {
if _, err := fmt.Fscan(reader, &stairs[i]); err != nil {
log.Fatal(err)
}
}
fmt.Fprintln(writer, dp(stairs, N-1))
}