[Programmers] Joystick (Golang)
Problem
Vervollständigen Sie den Namen mit dem Joystick. Am Anfang besteht alles nur aus A.
z.B.) Wenn der zu vervollständigende Name drei Buchstaben hat, dann AAA, wenn vier Buchstaben, dann AAAA
Indem Sie den Joystick in jede Richtung bewegen, sieht es folgendermaßen aus:
▲ - Nächster Buchstabe
▼ - Vorheriger Buchstabe (wenn man von A nach unten geht, ist es Z)
◀ - Den Cursor nach links bewegen (wenn man an der ersten Position nach links geht, ist der Cursor am letzten Zeichen)
▶ - Den Cursor nach rechts bewegen (wenn man an der letzten Position nach rechts geht, ist der Cursor am ersten Zeichen)
Zum Beispiel kann man "JAZ" mit der folgenden Methode erstellen:
- Bewege den Joystick 9 Mal nach oben, um J zu vervollständigen.
- Bewege den Joystick einmal nach links, um den Cursor an die letzte Zeichenposition zu bewegen.
- Bewege den Joystick einmal nach unten, um Z zu vervollständigen.
Deshalb kann man "JAZ" mit 11 Bewegungen erstellen, und dies ist die minimale Bewegung.
Erstellen Sie eine Funktion namens solution, die die minimale Anzahl der Joystickmanipulationen für den gegebenen Namen name als Parameter zurückgibt.Dieses Problem ist im Ausdrucksteil des Coding-Tests als LEVEL2 kategorisiert, aber ich fand es unerwartet schwierig, sodass ich mich fragte, warum es LEVEL2 ist.
Für mich war es eher LEVEL3.
Ansatz
Dieses Problem kann grob in 2 Teile unterteilt werden.
- Den Joystick nach oben/unten bewegen, um Buchstaben zu vervollständigen.
- Den Joystick nach links/rechts bewegen, um den Cursor zu verschieben.
Der erste Teil ist einfacher als erwartet, während der zweite Teil schwieriger ist.
1. Den Joystick nach oben/unten bewegen, um Buchstaben zu vervollständigen
Das Vervollständigen von Buchstaben mit dem Joystick nach oben/unten ist einfacher als erwartet. Dies kann angegangen werden, indem man die Vor- und Rückwärtsbewegungen in Betracht zieht und das Minimum ermittelt.
package main
func min(arr ...int) int {
value := arr[0]
for _, n := range arr {
if n < value {
value = n
}
}
return value
}
func solution(name string) int {
verticalMove := 0
for _, alpha := range name {
asc := int(alpha - 'A')
desc := int('Z' - alpha + 1)
verticalMove += min(asc, desc)
}
// ... auslassen
}Der Ausgangswert wurde als vollständig aus A bestehend betrachtet, was bedeutet, dass es in aufsteigender Reihenfolge 0 für A und 1 für B hätte.
Ein einfacher ASCII-Wert würde es ermöglichen, das wie folgt zu berechnen: Wenn alpha - 'A' für alpha gleich A ist, wäre es 0, für B wäre es 1, für C wäre es 2 usw.
Der rückwärtige Wert kann als Z - alpha + 1 berechnet werden. Man muss +1 hinzufügen, denn selbst wenn Z zu alpha minus alpha ist, ist es 0, es erfordert jedoch aufgrund des Joysticks 1 Manipulation.
Hier habe ich die Funktion min zusätzlich definiert. Tatsächlich ist die min-Funktion auch eine Standardbibliotheksfunktion in Go, aber bei Programmers wird eine sehr veraltete Version Go 1.16.9 verwendet, weshalb ich sie selbst definieren musste.
Übrigens wird die
min-Funktion ab Go 1.21 als Standardbibliotheksfunktion bereitgestellt.
2. Den Joystick nach links/rechts bewegen, um den Cursor zu verschieben
In diesem Bereich hatte ich unerwartet Schwierigkeiten.
Ich schreibe diesen Reflexionsbeitrag, weil ich Hilfe von ChatGPT erhalten habe.
Das Problem sind die aufeinanderfolgenden A, da die Bedingung des Problems besagt, dass A automatisch als Anfangswert gefüllt wird, was dazu führen kann, dass die minimale Anzahl an Bewegungen des Cursors je nach Richtung, in die man den Joystick bewegt, variieren kann.
Beispielanstich: AAAA
Nehmen wir an, wir schreiben den Namen AAAA
In diesem Fall muss der Name nicht eingegeben werden, denn es ist bereits mit A gefüllt.
Beispielanstich: AABA
Jetzt nehmen wir an, wir versuchen den Namen AABA zu schreiben.
In diesem Fall gibt es zwei Möglichkeiten, zuerst nach links und dann nach rechts zu bewegen oder zuerst nach rechts und dann nach links.
Wenn man nach links bewegt, sind die ersten zwei A bereits vervollständigt, sodass man nur den Cursor 2 Mal nach rechts und einmal nach oben bewegen muss, um AABA zu vervollständigen. Insgesamt sind es 3 Manipulationen.
Wenn man nach rechts bewegt, muss man zuerst den Cursor einmal nach links bewegen und dann einmal nach oben, um AABA zu vervollständigen. Insgesamt sind es nur 2 Manipulationen.
Dieses Beispiel ist relativ einfach, aber es gibt auch kompliziertere Beispiele.
Beispielanstich: BBBAAAAAAAAAB
Nehmen wir an, wir versuchen den Namen BBBAAAAAAAAAB zu schreiben. Wenn wir wie zuvor nur in aufsteigender Reihenfolge gehen, wären es 2 Mal nach oben, 11 Mal nach rechts, 1 Mal nach oben, was 14 Manipulationen erfordert.
Wenn wir nur in absteigender Reihenfolge gehen, wären es ebenfalls 14 Manipulationen: 2 Mal nach oben, 11 Mal nach links, 1 Mal nach oben.
Aber was, wenn wir nur BBB eingeben und dann zurückkehren?
In diesem Fall wären es 3 Mal nach oben für den Cursor, 2 Mal für den Cursor nach rechts und 3 Mal nach links für den Cursor, was bedeutet, dass ich insgesamt 9 Manipulationen benötigen würde, um das letzte B zu ändern.
Was wäre, wenn wir zuerst in die entgegengesetzte Richtung gehen und dann zurückkehren?
In diesem Fall wären es 1 Mal nach links, 1 Mal nach oben für das B, 1 Mal nach rechts für den Cursor zurückzukehren und dann 3 Mal nach oben, 2 Mal nach rechts, was insgesamt 8 Manipulationen erfordert.
So variiert die Anzahl der Joystickbewegungen nach links/rechts je nach Position und dem Vorkommen von aufeinanderfolgenden A.
Um dieses Problem zu lösen, sollten wir beim Verschieben des Cursors nach jedem Schritt berücksichtigen, wie bis zum nächsten A bewegt werden kann und auch in umgekehrter Reihenfolge, um mit einer greedschen Methode das Minimum zu ermitteln.
Code
Lassen Sie uns den Code zunächst ansehen und ihn Schritt für Schritt aufschlüsseln.
package main
func solution(name string) int {
// ... auslassen
horizontalMove := len(name) - 1
for i := 0; i < len(name)-1; i++ {
next := i + 1
for next < len(name) && name[next] == 'A' {
next++
}
// Rechts gehen und dann zurück und nach links bewegen
moveRightLeft := (i * 2) + (len(name) - next)
// Nach links gehen, zurück und nach rechts bewegen
moveLeftRight := (len(name)-next)*2 + i
horizontalMove = min(horizontalMove, moveRightLeft, moveLeftRight)
}
// ... auslassen
}Zunächst ist der maximale Wert für horizontalMove die Länge des Namens minus eins. Dies bedeutet, dass es sich um den Fall handelt, bei dem man sich ohne Richtungswechsel vom ersten zum letzten Zeichen bewegt.
horizontalMove := len(name) - 1Danach definieren wir next. Wenn next A ist, bewegen wir den Cursor so lange, bis wir das Ende des A erreichen, um die minimale Cursorbewegungsanzahl basierend auf der Differenz zwischen next und i zu ermitteln.
next := i + 1
for next < len(name) && name[next] == 'A' {
next++
}Nachdem wir moveRightLeft und moveLeftRight berechnet haben.
// Rechts gehen und dann zurück und nach links bewegen
moveRightLeft := (i * 2) + (len(name) - next)
// Nach links gehen, dann zurück und nach rechts bewegen
moveLeftRight := (len(name)-next)*2 + iWie der Name schon sagt, bedeutet moveRightLeft, dass man nach rechts geht, dann um i zurück und dann nach links um len(name) - next bewegt.

Die abgebildeten Zahlen 1 und 2 zeigen die Bewegungen von jeweils i, während 3 sich darauf bezieht, wie weit man für len(name) - next geschätzt werden kann.
Umgekehrt bedeutet moveLeftRight, dass man zunächst um len(name) - next nach links geht, dann um len(name) - next zurück, und schließlich nach rechts um i geht.
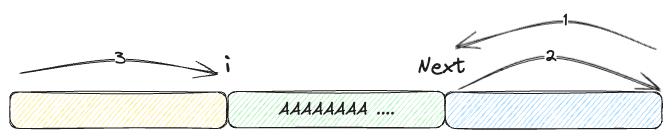
Die Zahlen 1 und 2 zeigen die Bewegungen von len(name) - next, während 3 sich auf die Bewegung auf i bezieht.
Daher kann der Algorithmus zur Berechnung von horizontalMove als eine Methode angesehen werden, die die minimalen Werte aus verschiedenen Bedingungen ermittelt:
- Bewegung nur in eine Richtung:
len(name) - 1 - Für jeden Index i nach rechts gehen und dann nach links zurück:
(i * 2) + (len(name) - next) - Für jeden Index i zuerst nach links gehen und dann nach rechts zurück:
(len(name)-next)*2 + i
Auf diese Weise kann die minimale Anzahl der Joystickmanipulationen für alle Indizes des Namens ermittelt werden.
Endgültiger Code
package main
import "fmt"
func min(arr ...int) int {
value := arr[0]
for _, n := range arr {
if n < value {
value = n
}
}
return value
}
func solution(name string) int {
verticalMove := 0
for _, alpha := range name {
asc := int(alpha - 'A')
desc := int('Z' - alpha + 1)
verticalMove += min(asc, desc)
}
horizontalMove := len(name) - 1
for i := 0; i < len(name)-1; i++ {
next := i + 1
for next < len(name) && name[next] == 'A' {
next++
}
// Rechts gehen und dann zurück und nach links bewegen
moveRightLeft := (i * 2) + (len(name) - next)
// Nach links gehen, zurück und nach rechts bewegen
moveLeftRight := (len(name)-next)*2 + i
horizontalMove = min(horizontalMove, moveRightLeft, moveLeftRight)
}
return verticalMove + horizontalMove
}
func main() {
case1 := solution("JEROEN")
fmt.Println(case1)
case2 := solution("JAN")
fmt.Println(case2)
}