[BOJ-9934] Vollständiger Binärbaum (Golang)
Überblick
Ich habe mich entschieden, diesen Beitrag zu schreiben, während ich mich auf einen Jobwechsel vorbereite und nach langer Zeit wieder die Baumalgorithmen studiere.
Das Problem des vollständigen Binärbaums ist ein Problem, bei dem die Form eines vollständigen Binärbaums anhand eines in-Order Traversierung anzuzeigenden Arrays ermittelt werden muss. Um dieses Problem zu lösen, sollte man zunächst das Konzept der in-Order Traversierung verstehen.
In-Order Traversierung
Die Kriterien für vor, in und nach der Traversierung basieren auf der Sichtweise des Knotens.
Knoten -> linkes Teilbaum -> rechtes Teilbaum bedeutet, dass der Knoten an erster Stelle steht, also ist es eine Vor-Order Traversierung,
linkes Teilbaum -> Knoten -> rechtes Teilbaum bedeutet, dass der Knoten in der Mitte steht, daher ist es eine In-Order Traversierung.
Linkes Teilbaum -> rechtes Teilbaum -> Knoten bedeutet, dass der Knoten am Ende steht und es sich somit um eine Nach-Order Traversierung handelt.
Hier betrachten wir die In-Order Traversierung, und ein Beispiel für die Traversierung sieht wie folgt aus:
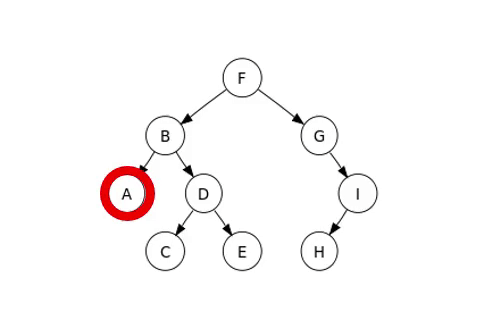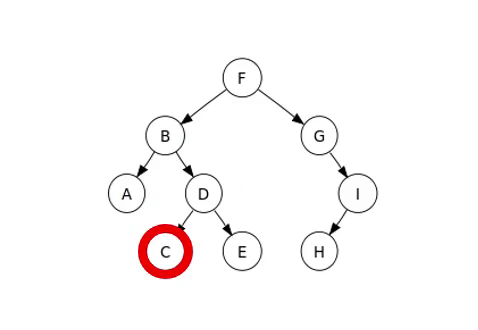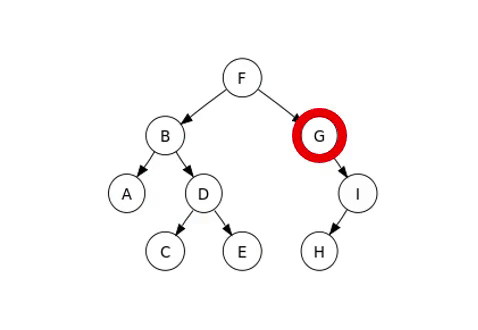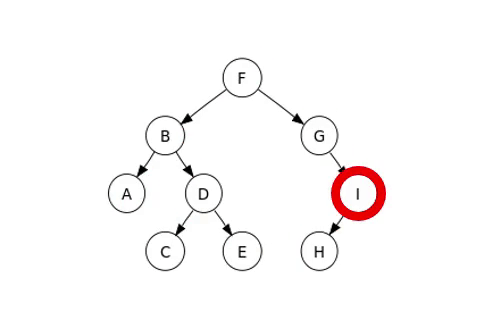
Vollständiger Binärbaum
Ein vollständiger Binärbaum ist ein binärer Baum, der die Bedingung erfüllt, dass die Gesamtzahl der Knoten N im Verhältnis zur Höhe h des Baums 2^h-1 ist.
Ein binärer Baum ist ein Baum, in dem die Anzahl der Kinder jedes Knotens maximal 2 betragen darf.
Einfach ausgedrückt bedeutet dies, dass der Baum auf der festgelegten Höhe voll besetzt ist.
Wenn wir beispielsweise einen Baum mit Höhe 1 betrachten, sind lediglich ein Knoten vorhanden, wie unten gezeigt.
Anzahl der Knoten = 2^1-1 = 1

Bei einer Höhe von 2 würden wir einen Baum mit 3 Knoten haben.
Problemlösung
Zunächst sollten wir uns das Ergebnis der In-Order Traversierung ansehen.
Der gegebene Baum sieht wie folgt aus,
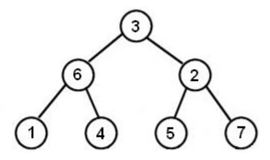
Das Beispiel für die In-Order Traversierung dieses Baums ist [1, 6, 4, 3, 5, 2, 7].
Wenn wir uns das Array ansehen, können wir erkennen, dass das Array in gewissem Maße wie ein Baum aussieht:

Wenn wir die Höhe allmählich ändern, was sehen wir dann?
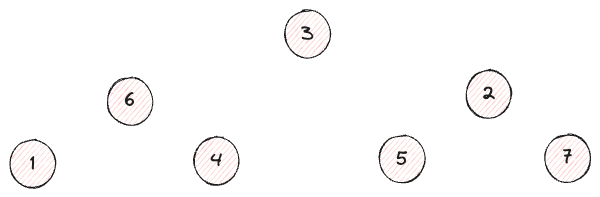
Es beginnt etwas sichtbar zu werden.
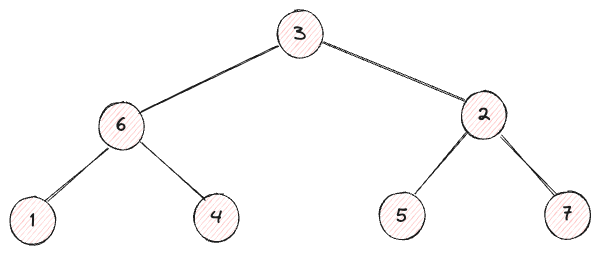
Wir können erkennen, dass es die Gestalt des Baums enthält, den wir erstellen möchten.
Jetzt lassen Sie es uns in Code umsetzen.
Da das Ziel dieser Aufgabe darin besteht, die Knoten nach Höhe auszugeben, müssen wir zuerst den Wurzelknoten finden.
1. Wurzelknoten finden
Der Wurzelknoten eines vollständigen Binärbaums kann sehr einfach gefunden werden. Wie bereits erwähnt, hat er immer eine Länge von 2^h-1, und da die Form des In-Order Traversierungsbaums selbst wie ein flach gedrückter Baum aussieht, befindet sich der Wurzelknoten immer in der Mitte.
In dem Array [1, 6, 4, 3, 5, 2, 7] ist das mittlere Element 3, was bedeutet, dass es der Wurzelknoten ist, wie wir zuvor im Bild gesehen haben.
In Code ausgedrückt wäre das:
root := arr[len(arr)/2]2. Kindknoten finden
Die Kindknoten können durch Teilen des Wurzelknotensindex nach links und rechts gefunden werden.
Betrachten wir das In-Order Traversierungsarray:
[1, 6, 4, 3, 5, 2, 7]. Die Kindknoten des Wurzelknotens sind 6 und 2.
Wir können sehen, dass jede dieser Knoten einen Abstand von 2 Indizes zum Wurzelknoten 3 hat.
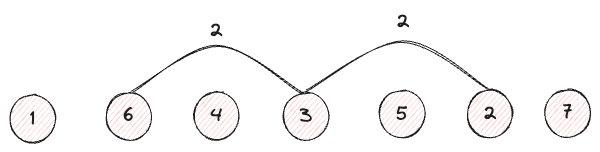
Schauen wir uns nun die Kindknoten von 6 und 2 an, diese sind 1, 4 und 5, 7 respectively.
Hier erkennen wir, dass sie jeweils einen Abstand von 1 Index zu 6 und 2 haben.
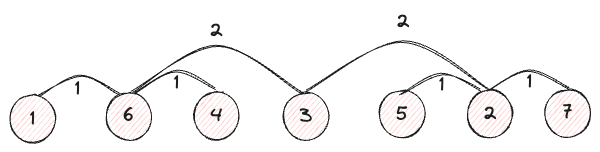
Wir können sehen, dass mit zunehmendem Abstand zu den Eltern der Abstand zwischen den Indizes abnimmt. Der spezifische Abstand ist jedoch noch unklar, also lassen Sie uns mehr Knoten hinzufügen und sie genauer untersuchen.
Angenommen, der In-Order Traversierungsergebnis besteht aus aufeinanderfolgend Zahlen:

Der Wurzelknoten ist der mittlere Knoten 8, und seine Kinder sind 4 und 12.
Wir können sehen, dass der Abstand zwischen den Indizes 4 beträgt.

Schauen wir uns die Kinder von 4 und 12 an, die Kinder von 4 sind 2, 6, während die Kinder von 12 10, 14 sind.
Hier beträgt der Abstand zwischen den Indizes jeweils 2.

Wenn wir die verbleibenden Knoten betrachten, sehen wir, dass die Kinder von 2 und 6 jeweils 1, 3 und 5, 7 sind, während die Kinder von 10 und 14 jeweils 9, 11 und 13, 15 sind. Auch hier beträgt der Abstand zwischen den Indizes 1.
Somit können wir erkennen, dass der Abstand zwischen den Indizes je nach Höhe variiert: an der Wurzel in Höhe 1 beträgt er 4, in Höhe 2 beträgt er 2 und in Höhe 3 beträgt er 1.
Mathematisch kann dieser Abstand für die gesamte Höhe des Baums K für die Höhe h wie folgt dargestellt werden:
interval = 2^(K-h)Planung
Lassen Sie uns die Schritte (a) den Wurzelknoten zu finden, (b) die Kinderknoten, die interval unterscheidet, durch den Wurzelknoten zu finden, und (c) die Kindknoten von diesen Kindknoten, ebenfalls unter Berücksichtigung des interval abzuleiten, zusammenfassen.
Lösung
Es gibt viele Punkte, die miteinander verbunden sind, um den Erklärungsteil in den Code zu unterteilen, daher werde ich sie durch Kommentare im Code ersetzen.
package main
import (
"bufio"
"fmt"
"log"
"os"
)
func main() {
writer := bufio.NewWriter(os.Stdout)
reader := bufio.NewReader(os.Stdin)
defer writer.Flush()
// Erhalte die Baumhöhe
var K int
if _, err := fmt.Fscanln(reader, &K); err != nil {
log.Fatal(err)
}
// Berechne die Baumlänge und lese das In-Order Traversierungsarray ein
length := 1<<K - 1
inOrder := make([]int, length)
for i := 0; i < length; i++ {
if _, err := fmt.Fscan(reader, &inOrder[i]); err != nil {
log.Fatal(err)
}
}
// initialer Index für Wurzelknoten: gesamte Länge / 2 ist der Wurzelknoten
idxs := []int{length / 2}
// Prozess um die Kindknotenindizes je nach Höhe h zu bestimmen (letzte Höhe hat keine Kinder, daher nur Speicherung in idxs für diesen Schritt)
for h := 1; h < K; h++ {
children := make([]int, 0, 1<<(h))
interval := 1 << (K - h - 1)
for _, idx := range idxs {
_, _ = fmt.Fprint(writer, inOrder[idx], " ") // Ausgabe der Kindknoten für die Höhe h
children = append(children, idx-interval, idx+interval) // Speichere die Kindknotenindizes
}
idxs = children
_, _ = fmt.Fprintln(writer)
}
// Ausgabe der letzten Höhe der Kindknoten
for _, idx := range idxs {
_, _ = fmt.Fprint(writer, inOrder[idx], " ")
}
}Ergebnis

Fazit
Auf diese Weise konnte ich das Problem des vollständigen Binärbaums lösen. Diese Lösungsmethode habe ich von einem anderen Beitrag inspiriert. Ursprünglich hatte ich die Methode verwendet, ein Dummy-Index-Baum zu erstellen und diesen in-Order zu traversieren, um dann basierend auf diesen Indizes den ursprünglichen Baum zu rekonstruieren.
Allerdings scheint mir diese Methode viel klarer und übersichtlicher zu sein, weshalb ich mich entschieden habe, diese Methode zu verwenden.
Im YangTaeyoung/algorithm können Sie den Algorithmus für dieses Problem, der in Go verfasst wurde sehen.