[프로그래머스] 조이스틱 (Golang)

문제

조이스틱으로 알파벳 이름을 완성하세요. 맨 처음엔 A로만 이루어져 있습니다.
ex) 완성해야 하는 이름이 세 글자면 AAA, 네 글자면 AAAA

조이스틱을 각 방향으로 움직이면 아래와 같습니다.

▲ - 다음 알파벳
▼ - 이전 알파벳 (A에서 아래쪽으로 이동하면 Z로)
◀ - 커서를 왼쪽으로 이동 (첫 번째 위치에서 왼쪽으로 이동하면 마지막 문자에 커서)
▶ - 커서를 오른쪽으로 이동 (마지막 위치에서 오른쪽으로 이동하면 첫 번째 문자에 커서)
예를 들어 아래의 방법으로 "JAZ"를 만들 수 있습니다.

- 첫 번째 위치에서 조이스틱을 위로 9번 조작하여 J를 완성합니다.
- 조이스틱을 왼쪽으로 1번 조작하여 커서를 마지막 문자 위치로 이동시킵니다.
- 마지막 위치에서 조이스틱을 아래로 1번 조작하여 Z를 완성합니다.
따라서 11번 이동시켜 "JAZ"를 만들 수 있고, 이때가 최소 이동입니다.
만들고자 하는 이름 name이 매개변수로 주어질 때, 이름에 대해 조이스틱 조작 횟수의 최솟값을 return 하도록 solution 함수를 만드세요.

해당 문제는 코딩 테스트 연습 파트에서 LEVEL2로 분류되어있는데, 사실 왜 LEVEL2일까 싶을 정도로 생각보다 내겐 어려운 문제였다.

~~내겐 LEVEL3 정도였다.~~

접근

해당 문제는 크게는 2파트로 나뉠 수 있다.

조이스틱을 위/아래로 움직여서 알파벳을 완성하는 부분
조이스틱을 좌/우로 움직여서 커서를 이동하는 부분

생각보다 1번은 쉽지만, 2번은 생각보단 어렵다.

1. 조이스틱을 위/아래로 움직여서 알파벳을 완성하는 부분

조이스틱을 위/아래로 움직여서 알파벳을 완성하는 부분은 생각보다 간단하다. 정순/역순 두가지를 고려하고 최솟값을 구해 더 해가는 방식으로 접근하면 된다.

package main

func min(arr ...int) int {
	value := arr[0]
	for _, n := range arr {
		if n < value {
			value = n
		}
	}
	return value
}

func solution(name string) int {
	verticalMove := 0
	for _, alpha := range name {
		asc := int(alpha - 'A')
		desc := int('Z' - alpha + 1)
		verticalMove += min(asc, desc)
	}
	
	// ... 생략
}

초기값은 문자열의 길이만큼 A로 채워져 있다고 했다. 그래서 정순 기준 만약 A라면 0이되고, B라면 1이된다. 아스키 값을 이용해서 간단히 계산하면 alpha-'A'라면 alpha값이 A라면 0, B라면 1, C라면 2가 되므로 조건을 만족할 수 있다.

역순은 Z - alpha + 1로 계산할 수 있다. 예를 들어 Z의 경우 만약 'Z' - alpha만 한다면 Z-Z이기에 0이지만, 조이스틱이기에 1번의 조작이 필요하므로 +1을 해준다.

여기서 필자는 min 함수를 추가로 정의했다. 사실 min함수는 Go의 표준 내장함수이기도 하지만, 프로그래머스에서는 Go 1.16.9 버전이라는 굉장히 오래된 버전을 사용하고 있기에, 직접 정의할 수 밖에 없다.

참고로 min 함수는 Go 1.21 버전부터 표준 내장함수로 제공된다.

2. 조이스틱을 좌/우로 움직여서 커서를 이동하는 부분

이 부분에서 필자는 생각보다 애를 많이 먹었다.

~~그래서 ChatGPT에게 도움을 받았기에 이 반성의 포스팅을 작성하고 있다.~~

문제는 연속된 A의 존재인데 초기값으로 A를 자동으로 채워준다는 문제의 조건이 있기에, 조이스틱을 움직이는 방향에 따라 커서가 이동해야 하는 최솟값이 달라질 수 있다는 점이다.

예시 케이스: `AAAA`

AAAA 라는 이름을 적는다고 해보자

이 경우 이름을 적을 필요가 없다. 이미 A로 채워져 있기 때문이다.

예시 케이스: `AABA`

그럼 AABA 라는 이름을 적는다고 해보자

이 경우 이 경우 왼쪽 -> 오른쪽으로 움직이는 방법과 오른쪽 -> 왼쪽으로 움직이는 방법이 존재한다.

왼쪽으로 움직이는 경우 AA까지는 이미 완성되어 있으므로, ▶ 커서만 2번 움직인 후 알파벳을 바꾸는 ▲ 커서 한번으로 AABA를 완성할 수 있다. 총 3번의 조작이 필요하다.

오른쪽으로 움직이는 경우 AABA를 완성하기 위해서는 커서를 왼쪽으로 1번 움직인 후, ▲ 커서 한번으로 AABA를 완성할 수 있다. 총 2번의 조작이 필요하다.

그나마 단순한 예시이지만 보다 복잡한 예시도 생각해볼 수 있다.

예시 케이스: `BBBAAAAAAAAAB`

예를 들어, BBBAAAAAAAAAB라는 이름을 적는다고 해보자, 앞선 예처럼 정순으로 가기만 한다면, ▲ 커서 2번, ▶ 커서 11번, ▲ 커서 1번으로 총 14번의 조작이 필요하다.

역순으로 가기만 한다면, ▲ 커서 2번, ◀ 커서 11번, ▲ 커서 1번으로 총 14번의 조작이 필요하다.

다만 BBB까지만 입력하고 돌아간다면 어떨까? 이 경우 B를 바꾸기 위한 커서 ▲ 3번, 정순으로 커서를 옮기기 위한 ▶ 2번, 다시 돌아가서 마지막 B로 옮기기 위한 커서 ◀ 3번, 마지막 B를 바꾸기 위한 ▲ 1번으로 총 9번의 조작이 필요하다.

또 역순을 먼저 옮기고 다시 돌아가는건 어떨까?

이 경우 마지막 B로 옮기기 위한 커서 ◀ 1번, B로 바꾸기 위한 ▲ 1번, 정순으로 커서를 옮기기 위한 ▶ 1번, B로 바꾸기 위한 커서 ▲ 3번, 우측으로 커서를 옮기기 위한 ▶ 2번으로 총 8번의 조작이 필요하다.

이처럼 조이스틱에 좌/우 이동은 연속된 A와 위치에 따라 최솟값이 달라질 수 있다.

그래서 이 부분을 해결하기 위해서는 매번 커서를 옮길 때마다, 다음 A가 나올 때까지 커서를 옮기는 방법과, 그 반대로 커서를 옮기는 방법을 모두 고려하여 그리디 방식으로 최솟값을 구해야 한다.

코드

이부분은 코드를 먼저 보고 하나하나 살펴보자

package  main

func solution(name string) int {
    // ... 생략
	horizontalMove := len(name) - 1
	for i := 0; i < len(name)-1; i++ {
		next := i + 1
		for next < len(name) && name[next] == 'A' {
			next++
		}
		// 오른쪽으로 갔다가 왼쪽으로 돌아와 왼쪽으로 이동하는 경우
		moveRightLeft := (i * 2) + (len(name) - next)
		// 왼쪽으로 갔다가 오른쪽으로 돌아와 오른쪽으로 이동하는 경우
		moveLeftRight := (len(name)-next)*2 + i

		horizontalMove = min(horizontalMove, moveRightLeft, moveLeftRight)
	}
	// ... 생략
}

먼저, horizontalMove의 최대 값은 len(name) - 1 이다. 이는 방향 변화 없이 커서를 처음 위치에서 끝 위치로 옮기는 경우를 의미한다.

horizontalMove := len(name) - 1

이후 next를 지정한다. next가 A인 경우 A가 끝나는 지점까지 커서를 옮겨서, next와 i의 차이를 이용해 최소 커서 이동 횟수를 구할 것이다.

next := i + 1
for next < len(name) && name[next] == 'A' {
    next++
}

이후 moveRightLeft와 moveLeftRight를 구한다.

// 오른쪽으로 갔다가 왼쪽으로 돌아와 왼쪽으로 이동하는 경우
moveRightLeft := (i * 2) + (len(name) - next)
// 왼쪽으로 갔다가 오른쪽으로 돌아와 오른쪽으로 이동하는 경우
moveLeftRight := (len(name)-next)*2 + i

이름에서도 알 수 있듯이 moveRightLeft는 오른쪽에서 i만큼 갔다가, 다시 i만큼 돌아오고, 왼쪽으로 len(name) - next만큼 이동하는 경우를 의미한다.

아래 그림으로 살펴보면 좀 더 쉽게 이해할 수 있을 것이다.

그림에서 1, 2번은 각각 i만큼 이동하며, 3번은 len(name) - next만큼 이동하는 경우를 의미한다.

moveLeftRight는 왼쪽으로len(name) - next만큼 갔다가, len(name) - next만큼 돌아오고, 오른쪽으로 i만큼 이동하는 경우를 의미한다.

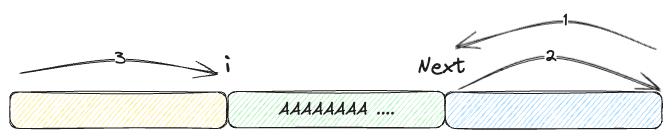
그림에서 1, 2번은 각각 len(name) - next만큼 이동하며, 3번은 i만큼 이동하는 경우를 의미한다.

그래서 결국 horizontalMove를 구하는 위 알고리즘은 다음의 경우의 수를 중 최솟값을 찾는 알고리즘이라 볼 수 있다.

단방향만 이동하는 경우: len(name) - 1
각 인덱스 i에서 오른쪽으로 이동 후 왼쪽으로 이동하는 경우: (i * 2) + (len(name) - next)
각 인덱스 i에서 왼쪽으로 이동 후 오른쪽으로 이동하는 경우: (len(name)-next)*2 + i

이렇게 하면 결국 name에 대한 모든 인덱스에서의 조이스틱 조작에 대한 최솟값을 구할 수 있다.

최종 코드

package main

import "fmt"

func min(arr ...int) int {
	value := arr[0]
	for _, n := range arr {
		if n < value {
			value = n
		}
	}
	return value
}

func solution(name string) int {
	verticalMove := 0
	for _, alpha := range name {
		asc := int(alpha - 'A')
		desc := int('Z' - alpha + 1)
		verticalMove += min(asc, desc)
	}

	horizontalMove := len(name) - 1
	for i := 0; i < len(name)-1; i++ {
		next := i + 1
		for next < len(name) && name[next] == 'A' {
			next++
		}
		// 오른쪽으로 갔다가 왼쪽으로 돌아와 왼쪽으로 이동하는 경우
		moveRightLeft := (i * 2) + (len(name) - next)
		// 왼쪽으로 갔다가 오른쪽으로 돌아와 오른쪽으로 이동하는 경우
		moveLeftRight := (len(name)-next)*2 + i

		horizontalMove = min(horizontalMove, moveRightLeft, moveLeftRight)
	}

	return verticalMove + horizontalMove
}

func main() {
	case1 := solution("JEROEN")
	fmt.Println(case1)
	case2 := solution("JAN")
	fmt.Println(case2)
}

[프로그래머스] 입국 심사 (Golang)[BOJ-2579] 계단 오르기 문제와 동적 프로그래밍 (Golang)