[BOJ-9934] 완전 이진 트리 (Golang)
개요
이직 준비를 하며 트리 알고리즘을 오랜만에 공부하다가 마주치게 되어 포스팅 하게 되었다.
완전 이진 트리 문제는 중위 순회한 순서 배열을 통해 완전 이진트리의 원형을 알아내어 출력하는 문제로 먼저 중위 순회라는 개념을 먼저 알아야 한다.
중위 순회
전위/중위/후위 순회의 기준은 노드의 시점을 보고 판단한다.
노드 -> 왼쪽 서브트리 -> 오른쪽 서브 트리 순서로 하면 노드가 앞에 있으니 전위 순회이며,
왼쪽 서브트리 -> 노드 -> 오른쪽 서브 트리 순서대로 하면 노드가 중간에 있으니 중위 순회이다
왼쪽 서브트리 -> 오른쪽 서브 트리 -> 노드 순서로 하면 노드가 가장 마지막에 있으니 후위순회이다.
이중에 살펴볼 방식은 중위 순회이며 순회하는 예시는 다음 이미지와 같다.
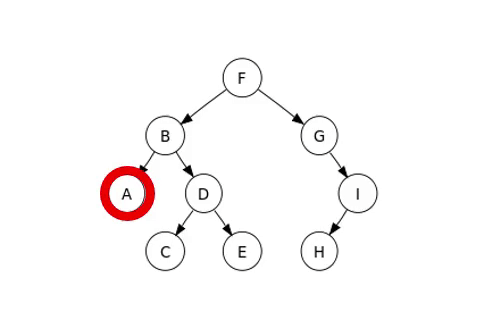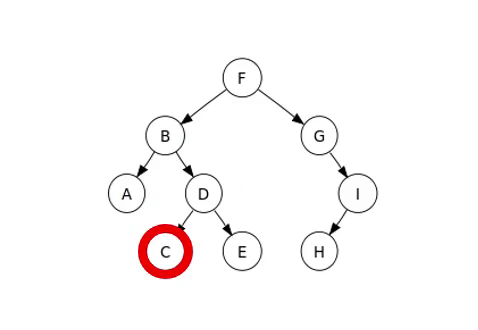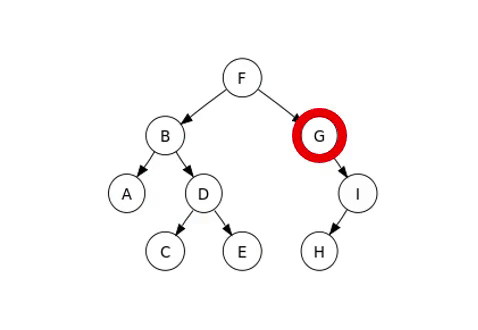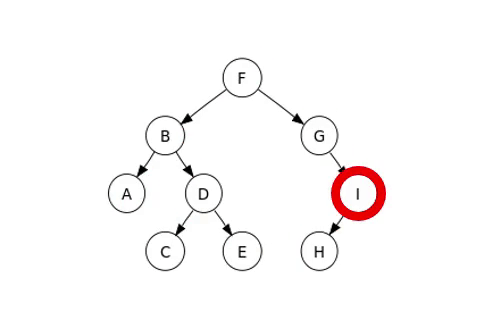
완전 이진트리
완전 이진트리는 트리 자료구조가 있을 때 트리의 높이 h에 대해 전체 노드 수가 2^h-1를 만족하는 이진 트리를 말한다.
이진 트리는 모든 노드의 자식의 수가 최대 2개가 됨을 만족하는 트리를 뜻한다.
쉽게 말하면 지정한 높이에 대해 모든 노드가 가득 찬 상태의 트리를 뜻한다.
예를 들어 높이가 1인 아래와 트리라면 단순히 아래 처럼 노드 하나만 있는 경우이다.
노드의 개수 = 2^1-1 = 1

높이가 2라면 다음과 같이 3개의 노드를 가진 트리가 된다.
문제 풀이
먼저 중위 순회한 결과를 살펴보자
문제에서 주어진 트리는 다음과 같고,
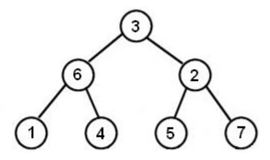
해당 트리를 중위 순회한 결과의 예시 입력은 [1, 6, 4, 3, 5, 2, 7]이다.
배열을 보면 배열 자체가 뭔가 트리처럼 생겼다는 걸 볼 수 있는데
다음과 같은 배열을,

높이를 조금씩 바꾸어보면?
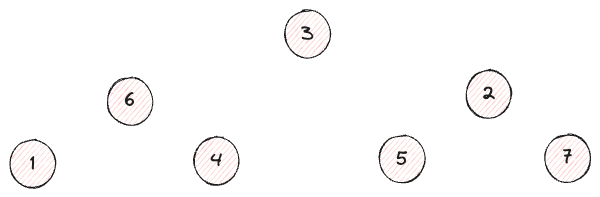
뭔가 보이기 시작한다.
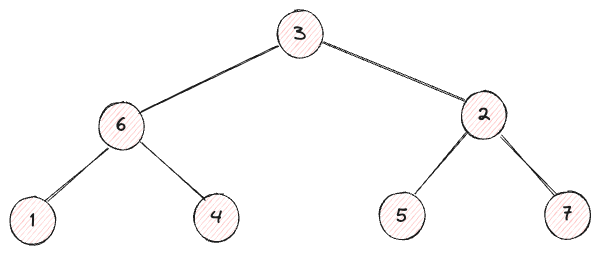
우리가 만들고자 한 트리의 모습을 그대로 담고 있는 것을 알 수 있다.
이제 이걸 코드 형태로 바꿔보자.
해당 문제는 높이 별 노드를 출력하는 것이 목적이기에 먼저 루트 노드를 찾아야 한다.
1. 루트 노드 찾기
완전 이진트리의 루트 노드는 매우 간단하게 찾을 수 있다. 앞서 말했듯이 항상 길이가 2^h-1 이며, 앞서 말했듯이 중위순회 트리 모양 자체가 트리 형태를 납작하게 눌러놓은 형태이기에 루트 노드는 항상 중앙에 위치한다.
다음 배열 [1, 6, 4, 3, 5, 2, 7]에서 중앙에 있는 요소는 3이며, 앞서 그림에서 확인한대로 루트노드임을 알 수 있다.
코드로 표현하면 다음과 같다.
root := arr[len(arr/2)]2. 자식 노드 찾기
자식 노드는 루트 노드의 인덱스를 기준으로 왼쪽과 오른쪽으로 나누어 찾을 수 있다.
중위 순회 배열을 한번 살펴보자
[1, 6, 4, 3, 5, 2, 7] 에서 루트 노드의 자식은 각각 6번과 2이다.
각각의 노드들은 루트 노드 3으로 부터 2개의 인덱스 차이를 두고 있는 것을 알 수 있다.
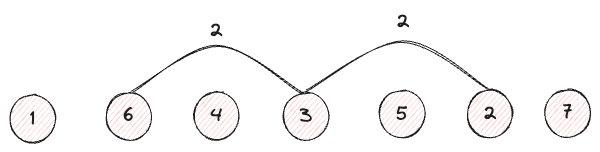
이제 자식의 자식을 살펴보자, 6과 2의 자식은 각각 1,4와 5,7이다.
이들은 각각 6과 2로부터 1개의 인덱스 차이를 두고 있는 것을 알 수 있다.
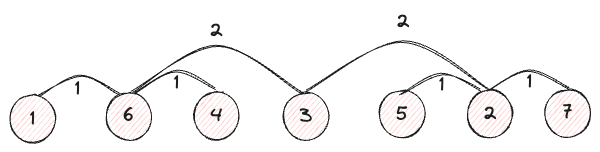
이렇게 부모로부터 떨어져 갈수록 인덱스 차이가 감소함을 알 수 있다. 다만 어떤 규칙으로 멀어지는 지는 아직 확인하기 어려움으로 다른 노드를 좀 더 추가해서 살펴보자
다음과 같이 이해를 쉽게 하기 위해 중위 순회한 결과가 연속되는 숫자로 되어 있다고 가정해보자

루트 노드는 중간인 8이며, 그의 자식은 각각 4, 12이다
각각의 인덱스 차이는 4임을 알 수 있다.

4와 12의 자식들을 알아보자, 4의 자식은 2, 6이며, 12의 자식은 10, 14이다.
각각의 인덱스 차이는 2임을 알 수 있다.

나머지를 보면 2와 6의 자식은 각각 1,3과 5,7이며, 10과 14는 각각 9,11과 13,15이다. 각각 인덱스 차이는 1임을 알 수 있다.
이처럼 인덱스가 차이가 나는 값은 높이에 따라 높이1인 루트에서는 4, 2번 높이에서는 2, 3번 높이에서는 1임을 알 수 있다.
이를 산식으로 표현해보면 전채 트리 높이 K에 대해 알고 싶은 높이 h의 인덱스 차이는 다음과 같다.
interval = 2^(K-h)설계
그럼 1,2을 종합해보자
먼저 (a)루트 노드를 찾고, (b)루트를 통해 interval만큼 떨어져있는 자식을 찾고 (c)해당 자식 노드를 이용해 자식노드의 자식에 대해 interval만큼 떨어져 있는 노드를 찾으면 될 것이다.
답안
설명을 코드 파트로 나누기엔 연관되는 부분이 많아, 코드 내 주석으로 대체한다.
package main
import (
"bufio"
"fmt"
"log"
"os"
)
func main() {
writer := bufio.NewWriter(os.Stdout)
reader := bufio.NewReader(os.Stdin)
defer writer.Flush()
// 트리 높이를 입력 받음
var K int
if _, err := fmt.Fscanln(reader, &K); err != nil {
log.Fatal(err)
}
// 트리높이를 통해 트리 길이를 구하고, 중위 순회 배열을 입력받음
length := 1<<K - 1
inOrder := make([]int, length)
for i := 0; i < length; i++ {
if _, err := fmt.Fscan(reader, &inOrder[i]); err != nil {
log.Fatal(err)
}
}
// 루트 노드의 초기 인덱스: 전체 길이 / 2는 루트 노드임
idxs := []int{length / 2}
// 높이 h에 따른 자식 노드의 인덱스를 구하는 과정(마지막 높이는 자식이 없으므로 해당 스탭에서는 idxs에만 저장)
for h := 1; h < K; h++ {
children := make([]int, 0, 1<<(h))
interval := 1 << (K - h - 1)
for _, idx := range idxs {
_, _ = fmt.Fprint(writer, inOrder[idx], " ") // 높이 h에 해당하는 자식 노드 출력
children = append(children, idx-interval, idx+interval) // 자식 노드 인덱스 저장
}
idxs = children
_, _ = fmt.Fprintln(writer)
}
// 마지막 높이의 자식 노드 출력
for _, idx := range idxs {
_, _ = fmt.Fprint(writer, inOrder[idx], " ")
}
}결과

마무리
이렇게 완전 이진 트리 문제를 해결할 수 있었다. 이 해결방법은 다른사람의 풀이를 보고 참조했는데, 필자의 경우 사실 처음에는 더미 인덱스 트리를 만들어서 중위 순회한 후, 해당 인덱스를 이용해서 기존 트리를 유추하는 방식으로 진행했었다.
다만 해당 방식이 코드 자체가 좀 더 간결하고, 깔끔한 것 같아 해당 방식을 차용했다.
YangTaeyoung/algorithm에서 필자가 작성한 해당 문제에 대한 Go로 작성된 알고리즘 문제 풀이 코드를 볼 수 있다.