[BOJ-2579] 계단 오르기 문제와 동적 프로그래밍 (Golang)
들어가며
사실 동적 프로그래밍을 너무 오랫동안 하지 않고, 예전에 했을 때도 그냥 이런게 있구나 정도로만 하고 넘어갔던 것이 문제였는지, 해당 문제는 손도 대지 못했던 문제였다.
이래서 이번에는 동적 프로그래밍을 제대로 공부해보자고 마음먹고, 문제를 풀어보았다.
동적 프로그래밍(Dynamic Programming)?
동적 프로그래밍(Dynamic Programming, DP)은 문제를 작은 하위 문제로 나누어 해결하는 알고리즘 설계 기법이다. 이 기법은 주로 최적화 문제에 사용되며, 중복되는 하위 문제를 효율적으로 해결하기 위해 메모이제이션(Memoization) 또는 테이블을 사용하여 이전 계산 결과를 저장하고, 재사용하는 방식으로 동작한다.
동적 프로그래밍은 다음과 같은 두 가지 주요 속성을 가지고 있다:
- 최적 부분 구조(Optimal Substructure): 문제의 최적 해결 방법이 하위 문제의 최적 해결 방법으로 구성될 수 있다.
- 중복되는 하위 문제(Overlapping Subproblems): 동일한 하위 문제가 여러 번 계산되는 경우가 있다.
대표적인 예로 피보나치 수열(Fibonacci Sequence) 계산이 있다. 피보나치 수열은 다음과 같은 점화식을 가진다.
$$f(n) = f(n - 1) + f(n - 2)$$
푸는 방식은 탑다운 방식과 바텀 업 방식이 있다. 탑다운 방식은 재귀를 사용하여 하위 문제를 해결하고, 바텀 업 방식은 반복문을 사용하여 하위 문제를 해결한다는 점에서 차이가 있다.
피보나치 수열을 구하는 것을 동적 프로그래밍을 이용하여 코드로 나타내면 다음과 같다
탑다운 방식 (Top-Down Approach)
package main
import "fmt"
var memo = make(map[int]int)
func fibonacci(n int,) int {
if n <= 1 {
return n
}
if val, exists := memo[n]; exists {
return val
}
memo[n] = fibonacci(n-1) + fibonacci(n-2)
return memo[n]
}
func main() {
n := 10
result := fibonacci(n)
fmt.Println("Fibonacci(", n, ") =", result)
}바텀 업 방식 (Bottom-Up Approach)
package main
import "fmt"
func fibonacci(n int) int {
if n <= 1 {
return n
}
fib := make([]int, n+1)
fib[0], fib[1] = 0, 1
for i := 2; i <= n; i++ {
fib[i] = fib[i-1] + fib[i-2]
}
return fib[n]
}
func main() {
n := 10
result := fibonacci(n)
fmt.Println("Fibonacci(", n, ") =", result)
}핵심 로직을 살펴보면, 탑다운 방식은 재귀와 메모이제이션 테이블 memo를 사용하여 중복되는 하위 문제를 해결하고, 바텀 업 방식은 반복문을 사용하여 하위 문제를 해결한다.
메모이제이션을 안쓰면?
사실 메모이제이션을 쓰지 않아도, 문제를 해결하는 데는 문제가 없다. 다만, 동적 프로그래밍 대상인 문제들은 항상 중복 되는 하위 문제가 존재하기 때문에, 메모이제이션을 사용하지 않으면 시간 복잡도가 기하급수적으로 증가하게 된다.
예를 들어보자.
피보나치 수열의 특정 값인 $f(5)$를 구하려면 어떻게 해야 할까?
다음과 같이 식으로 표현할 수 있다. $$f(5) = f(4) + f(3)$$
그리고 f(4)를 구하기 위해서는 다음과 같이 표현할 수 있다.
$$f(4) = f(3) + f(2)$$
이제 두 산식을 살펴보자. 주목할 부분은 $f(3)$이다. $f(3)$은 $f(4)$와 $f(5)$를 구하기 위해서 두 번 호출되었다.
피보나치 수열에서는 최대 중복 횟수가 2회로 제한되지만, 다른 동적 프로그래밍에서는 때에 따라서는 중복 횟수가 기하급수적으로 증가할 수 있다.
이런 것들 참조하여 다음 문제인 계단 오르기 문제를 풀어보자.
문제
계단 오르기 게임은 계단 아래 시작점부터 계단 꼭대기에 위치한 도착점까지 가는 게임이다. <그림 1>과 같이 각각의 계단에는 일정한 점수가 쓰여 있는데 계단을 밟으면 그 계단에 쓰여 있는 점수를 얻게 된다.
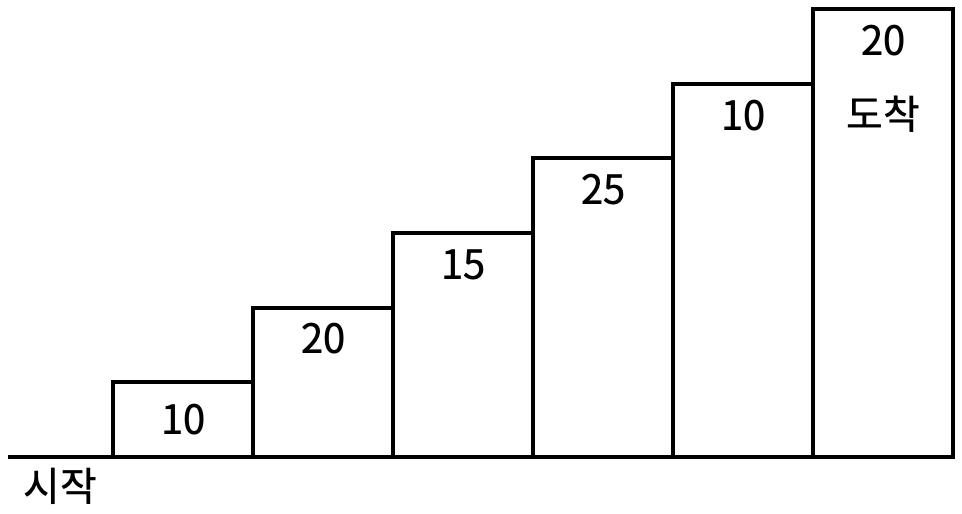
<그림 1>
예를 들어 <그림 2>와 같이 시작점에서부터 첫 번째, 두 번째, 네 번째, 여섯 번째 계단을 밟아 도착점에 도달하면 총 점수는 10 + 20 + 25 + 20 = 75점이 된다.
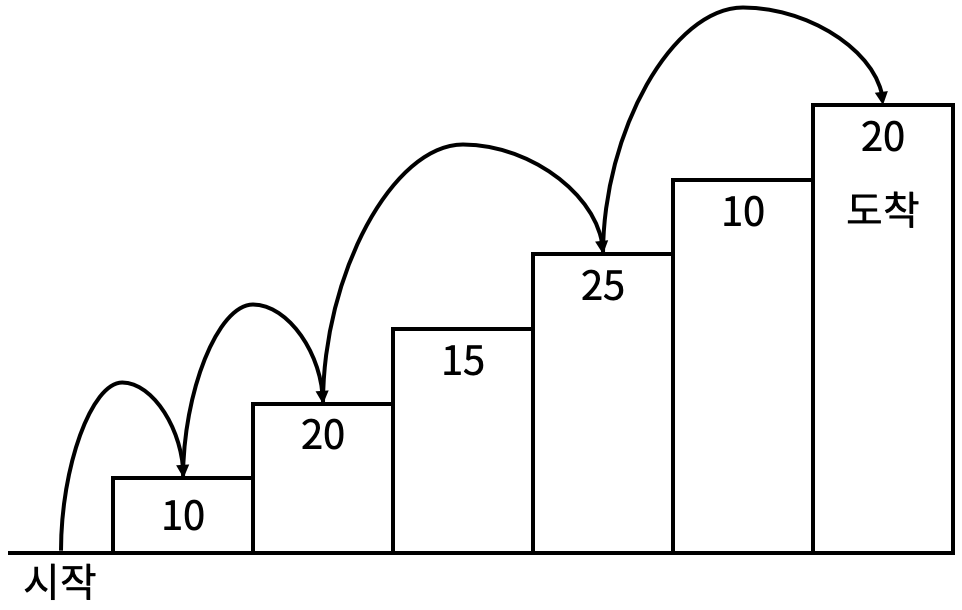
<그림 2>
계단 오르는 데는 다음과 같은 규칙이 있다.
계단은 한 번에 한 계단씩 또는 두 계단씩 오를 수 있다. 즉, 한 계단을 밟으면서 이어서 다음 계단이나, 다음 다음 계단으로 오를 수 있다. 연속된 세 개의 계단을 모두 밟아서는 안 된다. 단, 시작점은 계단에 포함되지 않는다. 마지막 도착 계단은 반드시 밟아야 한다. 따라서 첫 번째 계단을 밟고 이어 두 번째 계단이나, 세 번째 계단으로 오를 수 있다. 하지만, 첫 번째 계단을 밟고 이어 네 번째 계단으로 올라가거나, 첫 번째, 두 번째, 세 번째 계단을 연속해서 모두 밟을 수는 없다.
각 계단에 쓰여 있는 점수가 주어질 때 이 게임에서 얻을 수 있는 총 점수의 최댓값을 구하는 프로그램을 작성하시오.
접근
문제를 대충 읽었을 때는 그냥 계단 다 올라가면 되는거 아닌가? 싶지만, 계단을 오르는 규칙을 보면, 연속된 세 개의 계단을 밟아서는 안 된다는 점이 문제의 핵심이다.
따라서 계단을 오르는 방법은 다음과 같이 크게 두 가지로 나눌 수 있다.
- 현재 계단을 밟고, 이전 계단을 밟지 않고, 그 전 계단을 밟는 경우
- 현재 계단을 밟고, 이전 계단을 밟는 경우
이 두 가지 경우를 모두 고려하여 최댓값을 구해야 한다.
먼저 n번째 계단에서의 점수 최댓값을 어떻게 구할 수 있을까?
위의 경우의 수를 생각해 보았을 때 2가지 경우로 나타낼 수 있다.
1번 케이스: n번째 계단 점수 + (n-2)번째까지의 계단 점수 최댓값

2번 케이스: n번째 계단 점수 + (n-1)번째 계단 점수 + (n-3)번째까지의 계단 점수 최댓값

2번 케이스에서 단순히 $n-1$번까지의 최댓값으로 지정하지 않은 이유는, $n-1$번째 계단을 밟았을 때, $n-2$번째 계단을 밟지 않았음을 확정 짓기 위함이다.
점화식
이를 각각의 점화식으로 나타내면 다음과 같다.
$$f(n) = \max(f(n-2) + s(n), f(n-3) + s(n-1) + s(n))$$
여기서 $f(n)$은 n번째 계단에서의 최댓값, $s(n)$은 n번째 계단의 점수를 의미한다.
초기값 지정은 점화식에 있는 $f()$ 내의 숫자 값이 가질 수 있는 최소값을 각각 지정해주어야 한다
즉 해당 점화식에서 함수 내부에 있는 숫자는 각각 $n-1$, $n-2$, $n-3$에 해당하는 값이므로, 초기값은 인덱스 최솟값 0, 1, 2에 대해 다음과 같이 지정되어야 한다.
이를 따라 전체 점화식을 정리하면 다음과 같다.
$$f(0) = s(0)$$ $$f(1) = s(0) + s(1)$$ $$f(2) = \max(s(0) + s(2), s(1) + s(2))$$ $$f(n) = \max(f(n-2) + s(n), f(n-3) + s(n-1) + s(n))$$
코드
점화식이 나왔으니, 코드를 작성하는 것은 크게 어렵지 않다.
이를 따라 전체 코드를 작성하면 다음과 같다.
package main
import (
"bufio"
"fmt"
"log"
"os"
)
var memo = make(map[int]int)
func dp(stairs []int, n int) int {
if value, ok := memo[n]; ok {
return value
}
if n == 0 {
return stairs[0]
}
if n == 1 {
return stairs[0] + stairs[1]
}
if n == 2 {
return max(stairs[0]+stairs[2], stairs[1]+stairs[2])
}
// 두 계단을 한꺼번에
case1 := dp(stairs, n-2) + stairs[n]
// 1칸씩 두 번 올라가는 경우
case2 := dp(stairs, n-3) + stairs[n-1] + stairs[n]
memo[n] = max(case1, case2)
return memo[n]
}
func main() {
writer := bufio.NewWriter(os.Stdout)
reader := bufio.NewReader(os.Stdin)
defer writer.Flush()
var N int
if _, err := fmt.Fscan(reader, &N); err != nil {
log.Fatal(err)
}
stairs := make([]int, N)
for i := 0; i < N; i++ {
if _, err := fmt.Fscan(reader, &stairs[i]); err != nil {
log.Fatal(err)
}
}
fmt.Fprintln(writer, dp(stairs, N-1))
}